Метод разделения многомерных, нормальных смесей

(По Петрову А.В.).

Алгоритм, позволяет провести классификацию многопризнаковых геофизических наблюдений на однородные, в смысле вектора среднего области, без знания конечного числа классов и с учетом корреляционных характеристик всего признакового пространства.

Алгоритм построен на принципах самообучения и позволяет решать задачу разделения сейсмического разреза на области с одинаковым значением вектора среднего по совокупности признаков. Конечное число классов (однородных в смысле вектора среднего областей) определяется автоматически в процессе работы алгоритма. Суть алгоритма заключается в следующем.

Считается, что вся совокупность наблюдений, включающая M трасс по N отсчетов на каждой, может быть разбита на J областей, в которых данные распределены многомерно нормально с вектором математического ожидания 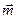и матрицей ковариаций S. Размерность векторов 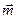и матрицы S совпадает с количеством анализируемых признаков p. Относительно ковариационной матрицы S предполагается, что она постоянна во всех областях. Вектора среднего 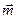для различных областей отличаются друг от друга, то есть

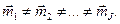
Число таких областей J ‑ неизвестно. Естественно, что оно не может быть меньше единицы (J>0) (в случае равенства единице все данные относятся к одной области, классу) и не превышает общего числа точек наблюдений J³MN=n (в случае равенства каждая область содержит только лишь один объект наблюдения, то есть точку). Задача заключается в разбиении исследуемой площади наблюдений на области, однородные в смысле вектора среднего, по всем признакам.

Для решения этой задачи предлагается алгоритм, основанный на проверке многомерной статистической гипотезы, в котором можно выделить два основных этапа:

1.На первом этапе проверяется гипотеза о принадлежности двух различных областей к одному классу. Первоначально считается, что число таких областей равно количеству точек наблюдений, то есть каждая точка ‑ класс. При этом, если два проверяемых класса удовлетворяют этой гипотезе на определенном уровне значимости, то они объединяются в один класс. Первоначальное число классов уменьшается на единицу и пересчитывается оценка ковариационной матрицы S, которая имеет важнейшее значение для расчета статистики критерия, соответствующего данной гипотезе. Этап завершается, когда гипотеза об объединении всевозможных пар классов не выполняется.

2.Второй этап заключается в реклассификации данных, разделенных на классы в результате первого этапа. Затем проводится повторение первого этапа, но при этом с самого начала в статистике критерия для проверки гипотезы объединения двух различных классов уже используется оценка ковариационной матрицы S, полученная на первом этапе обработки.

Как следует из структуры описанного алгоритма для его реализации необходимо получить многомерный статистический критерий для проверки гипотезы о том, что два любых класса m и l из J существующих, обладают одним и тем же вектором среднего, то есть гипотезу

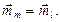
В работе [5] подробно описывается построение критериальной статистики для проверки сформулированной выше гипотезы, поэтому ниже приводится лишь окончательное выражение:

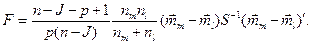
здесь n ‑ общее число точек;

n_m и n_l – число точек в проверяемых классах;

J – общее число классов;

p –число анализируемых признаков;

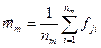‑ оценка вектора среднего в m ‑ом классе;

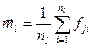‑ оценка вектора среднего в l ‑ом классе;

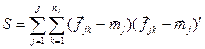- оценка ковариационной матрицы по всем классам;

n_j - число точек в j–ом классе.

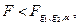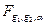Гипотеза H₁ о равенстве векторов средних в классах l и m считается справедливой на уровне значимости a. если выполняется неравенство: где ‑ критическое значение F ‑ распределения со степенями свободы: g₁ = p. g₂=n-J-p+1.