Методы распознавания образов в задачах интерпретации геофизических наблюдений.

Одной из актуальных задач разведочной геофизики является выделение геологического объекта по информации о параметрах полей, которые им индуцируются. Подобные задачи возникают при геолого-геофизическом районировании, обработке многоуровневых геофизических наблюдений и в других случаях, когда при интерпретации наблюденное поле сравнивается с эталонным фрагментом поля.

Существует ряд алгоритмов распознавания по данным комплексных геолого-геофизических наблюдений, в которых решение задачи коротко сводится к следующему. Первоначально проводится обучение на эталонных объектах по ряду геолого-геофизических признаков с целью оценки тех или иных параметров признаков. Затем по имеющейся информации о значениях параметров признаков в каждой точке площади исследования делается вывод о принадлежности точки к эталонному объекту. Этап обучения на эталонных объектах является одним из самых уязвимых мест рассматриваемых методов распознавания. Многообразие геолого-геофизической информации, обусловленное изменением геологического строения в пределах даже одной площади, влияние различного рода помех очень часто не позволяют использовать результаты обучения на эталонных объектах для решения задач распознавания на других площадях со сходным геологическим строением.

В наибольшей степени сказанное проявляется при включении в процесс распознавания геофизических наблюдений. Именно поэтому геофизическая информация обычно используется далеко не полностью и сводится чаще всего к таким параметрам, как знак аномалии, значение величины среднего, степень изменчивости полей (дисперсия) и их производных.

Параметрами, характеризующими эталонный объект для предлагаемого алгоритма, являются двумерные поверхности, заданные в дискретных точках наблюдений прямоугольной сети. Каждая поверхность отражает форму проявления конкретного физического поля над эталонным объектом. Признаками могут быть значения различных геофизических полей, их производные, наблюдения на различных уровнях одного геофизического параметра, оцифрованная геологическая, петрофизическая и геохимическая информация. При построении алгоритма принимается аддитивная модель поля, при которой любое наблюдение является суммой комплексной аномалии и многомерной нормальной с нулевым вектором среднего помехи.

Существо предлагаемого алгоритма состоит в следующем. Без ограничения общности рассмотрим прямоугольное окно на анализируемой площади наблюдений размером т профилей и n пикетов и наклоном q=0. Пусть в каждой i-ой точке окна наблюдения являются р - мерными величинами (р—число анализируемых признаков) fi= (f₁. f₂. .... f_р), причем: f_i=a_i+n_i, гдеa_i- аномальная составляющая поля, n_i-многомерная нормальная помеха с нулевым вектором среднего и матрицей ковариаций S.

Очевидно, при совпадении формы комплексной аномалии в исследуемом окне от эталонного объекта a с наблюденным полем x , разность между ними есть не что иное, как помеха:

d_kj= x_kj- a_kj где . k=1.2....... m; j=1.2....... п.

где m – количество строк в окне, а n –количество столбцов.

Таким образом, решение вопроса распознавания комплексной аномалии от эталонного объекта сводится к проверке нулевой гипотезы H₀о том, что значения разности d в столбцах и строках окна распределены нормально с нулевым вектором среднего и ковариационной матрицей S. т. е.

m₁=m₂=. . . . m_m= m_m+1 =. . . . .=m_m+n

где m_k. k=1....m - вектор среднего разности d в строках окна;

j=1....n—вектор среднего разности d в столбцах окна.

Окончательное выражение для проверки гипотезы H₀ [4] имеет вид:

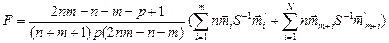
здесь

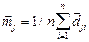-оценка вектора среднего разности в j-ой строке окна j=1.....m;

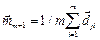-оценка вектора среднего разности в i-омстолбце окна i=1.....n.

S - оценка ковариационной матрицы в окне.

Гипотеза Н₀о наличии в окне эталонной комплексной аномалии считается справедливой на уровне значимости а. если выполняется неравенство F<F g _{1. g2}.a. а. где Fg₁.g₂.a -критическое значение F-распределения со степенями свободы g₁и g₂

.

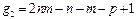Перемещая окно вдоль профиля и по профилям, получим распределение критериальной. статистики по всей площади наблюдения.

При использовании рассмотренного способа распознавания комплексных геофизических аномалий эталонную аномалию по комплексу признаков можно получить путем обучения на площадях с известным геологическим строением, либо путем решения прямой задачи по каждому признаку, а также создав банк элементарных аномалий, из которых путем линейных преобразований и различных комбинаций по признакам можно быстро получать комплексную аномалию с заданными энергией и геометрией. За эталонную аномалию можно принять фрагмент исследуемой площади с целью поиска аналогичных участков на всей площади. Особый интерес представляет распознавание при различных наклонах окна, так как при этом выделяются области в которых присутствует эталонный объект при различных его простираниях. Основные достоинства рассмотренного метода распознавания заключаются в следующем:

1.Алгоритм базируется на проверке многомерной статистической гипотезы, что позволяет наиболее полно использовать информацию о структуре межпризнаковой связи между различными геофизическими полями.

2.Исходной информацией является лишь форма аномалий, а в ряде случаев, когда эталоном служит фрагмент исследуемой площади, лишь контур комплексной аномалии. Оценка параметров помехи и ее влияния на полезный сигнал проводятся непосредственно в процессе распознавания.

3.В качестве признаков над эталонным объектом выступают геофизические поля, что позволяет наиболее полно учесть все их особенности при обработке.

4.Возможность изменения наклона окна делает алгоритм независимым от простирания объекта.

5.Независимость алгоритма от характера помех и применение банка элементарных аномалий значительно сокращают этап обучения и повышают мобильность алгоритма при обработке различных исследуемых территорий.

Основные недостатки метода сводятся к возможному невыполнению на практике предпосылок, заложенных в математической модели, а именно: принимаемая аддитивная модель наблюдаемого поля, предположение о нормальном распределении помехи и стохастическая независимость наблюдений.