Метод главных компонент при расчете комплексного параметра.

Исходными данными при комплексном анализе является совокупность нескольких полей и (или) их атрибутов в виде Nn-точек наблюдений. Алгоритм метода главных компонент сводится к реализации следующих процедур:

1.Вычисление коэффициентов корреляции 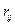для случайных величин 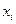и и 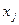составление по коэффициентам корреляции корреляционной матрицы

.

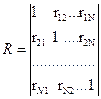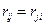
2.Составление матрицы 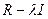. где I-единичная матрица, и приравнивание определителя матрицы 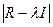к нулю, т.е.

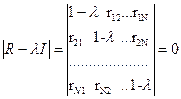
3.Раскрытие определителя 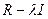в виде линейного уравнения относительно 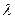и нахождение корней этого уравнения, являющихся собственными значениями матрицы .

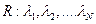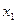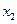Например, для двух случайных величин и имеем

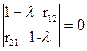
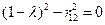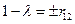; . т.е. ; .

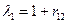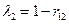Очевидно, что для матрицы R размерности N получим N собственных ее значений.

4.Нахождение собственных векторов 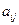матрицы R путем решения системы линейных уравнений вида:

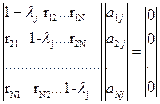
т.е.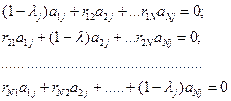

Для определенности решения этой системы необходима указанная выше нормировка коэффициентов 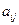в виде .

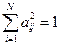В результате решения системы линейных уравнений для каждого собственного значения 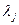получаем свой собственный вектор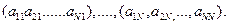

Система собственных векторов является ортогональной и корреляционная матрица R оказывается расщепленной на N-ортогональных компонент.

5.Вычисление первой главной компоненты 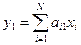, соответствующей максимальному собственному значению 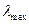. 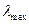равно дисперсии первой главной компоненты, отражающей 70-90% всей энергии. т.е. .

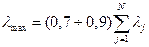Первая главная компонента представляет значения комплексного параметра, определяемого в n-точках наблюдений, поскольку 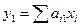выражается в виде произведения исходной матрицы x на собственный вектор, соответствующий максимальному собственному значению:

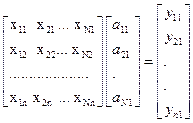
Физический смысл весовых коэффициентов 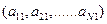состоит в том, что эти коэффициенты определяют «вес» (вклад) каждого поля в общую величину комплексного параметра или информативность исходных полей.

Заметим, что случайная природа полей практически в методе главных компонент не используется, поэтому все перечисленные выше процедуры можно использовать и для аналитических, детерминированных функций. Так, в метеорологии метод главных компонент получил название как метод естественных ортогональных функций.

ЗАКЛЮЧЕНИЕ.

В заключении отметим, что в процессе изучения материала по курсу «Теоретические основы обработки геофизической информации» следует использовать программные средства по соответствующим разделам, что способствует лучшему усвоению достаточно сложных теоретических основ.

В качестве подобных программных продуктов можно рекомендовать пакет «МАТLAB». В РГГРУ под руководством профессора Петрова А.В. разработаны обучающая система «Геостат» и компьютерная технология «КОСКАД 3D». Последняя включает шесть основных разделов:

«Сервис» -обеспечивает выполнение стандартных функций системы управления базой данных. С их помощью осуществляется ввод/вывод содержательной информации, объединение и фрагментация сетей, восполнение отсутствующих в отдельных точках наблюдения значений признака, интерполяция сетей, различные преобразования с данными и т.д.

«Графика»- включает графический интерфейс, позволяющий оперативно просматривать одномерную, двумерную и трехмерную информацию из базы данных на экране дисплея в виде растровых карт, отдельных графиков, карт графиков и т.д..

«Статистика»- программы данного раздела предназначены для расчета статистических, спектральных и корреляционных характеристик геополей. Анализ этих характеристик позволяет получить дополнительную, полезную информацию об исследуемом поле и правильно выбрать граф его дальнейшей обработки.

«Фильтрация» - в модулях данного раздела реализованы наиболее распространенные в разведочной геофизике линейные оптимальные фильтры, позволяющие решать задачи разложения поля на составляющие, исключения тренда, оценки формы слабых аномалий. Особый интерес представляют уникальные адаптивные фильтры, позволяющие корректно обрабатывать нестационарные по спектрально-корреляционным характеристикам геофизические поля.

«Обнаружение» -с помощью программ данного раздела решается задача обнаружения слабых аномалий, соизмеримых по амплитуде с уровнем помех, линейной и изометричной формы, по одному или нескольким признакам.

«Комплекс»-использование программ этого раздела позволяет решать задачи разбиения анализируемой площади на однородные области (классы) с равными средними значениями признаков, распознавания комплексных аномалий по эталонной аномалии. Кроме этого возможно проведение компонентного анализа многопризнаковых данных.

Для программ этой группы в качестве входной информации могут быть использованы значения различных геолого-геофизических признаков и их производных, полученных с помощью программ из других разделов комплекса.

[1] В главе 2 подробно рассматриваются метод наименьших квадратов и вопросы полиномиальной аппроксимации геофизических наблюдений.

[2] Слово correlationпереводится с английского языка как схожесть в изменениях, таким образом, под корреляцией понимается степень схожести или связи в изменении двух процессов.

[3]Если из значений случайной величины вычесть ее математическое ожидание (среднее), то полученная таким образом, случайная величина называется центрированной.

[4] Обычно получают достаточно достоверные оценки автокорреляционных функций при N>=30. При этом оценки вычисляются для смещений, не превышающих половины длины реализации (профиля) m<=N/2.

[5]Слово correlationпереводится с английского языка как схожесть в изменениях, таким образом, под корреляцией понимается степень схожести в изменениях двух процессов.

[6] что является далеко нетривиальной задачей.

[7] Под базовым окном понимается окно, размер которого не меньше наиболее энергоемких и протяженных аномалий, присутствующих на профиле. По точкам, попадающим в это окно, оцениваются корреляционные характеристики поля в окрестности каждой точки.

[8] Под двумерным базовым окном понимается прямоугольное окно, размеры которого не меньше размеров наиболее энергоемких аномалий.