Методом общего расстояния.

Алгоритм классификации методом общего расстояния является типичным примером эвристического алгоритма, основная идея которого заключается в том, что совокупность объектов, находящихся на одинаковом расстоянии от каждого из k эталонов, образует компактную группу.

Пусть для классификации имеется выборка A₁.….A_N. представленная в виде матриц размером в m профилей и n пикетов, причем каждый объект этой выборки характеризуется вектором признаков 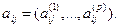Рассмотрим р - мерное признаковое пространство X^p вместе с функцией 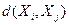, задающей расстояние (или степень близости). Здесь степень близости определяется как обычное евклидово расстояние:

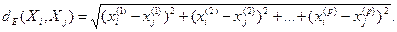
Тогда схема алгоритма имеет вид:

-для всех 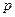обрабатываемых признаков оценивается среднее значение:

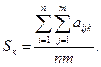
-каждый признак центрируется на соответствующее значение среднего a_ijk = a_ijk - S_к.

-для всех 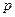обрабатываемых признаков оценивается значение среднеквадратического отклонения:

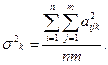
-каждый признак нормируется на соответствующее значение среднеквадратического отклонения:

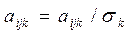
-для каждого из признаков выбирается 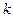эталонов .

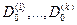-рассчитывается матрица (для каждого признака) средних расстояний от объекта до эталонов.

-выбирается общий порог d₀ .

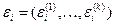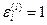-осуществляется классификация приведенных к однородности признаков по правилу, каждому объекту X_i ставится в соответствие код из k двоичных символов . где . если 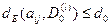. где l=1.....k и 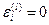в противном случае.

Выборка разбивается на классы. Объекты, относящиеся к одному классу, имеют одинаковый код.

Существенно повысить качество конечной классификации данного алгоритма позволяет учет следующих замечаний:

1.Нормировка данных по каждому признаку только на обычную дисперсию, из-за специфики геофизических наблюдений, для которых характерно наличие “ураганных” значений, не позволяет решать задачу нормировки корректно. Как показали исследования, качество классификации значительно улучшается, если стандартную нормировку на дисперсию, дополнить нормировкой на межэталонную дисперсию:

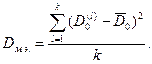
2.Мера сходства, также является важнейшим фактором качества классификации. Наиболее эффективным является следующий подход решения этой задачи:

-по каждому признаку рассчитываются средние расстояния от всех анализируемых точек исходной сети до эталонов s₁=…=s_p.

-находится общее среднее по всем признакам .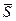

-величина 0.3 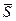, в качестве меры сходства, как показало опробование алгоритма на модельных и реальных данных, является наиболее приемлемым.