Методы классификации многомерных наблюдений.

Существующие в настоящее время классификационные алгоритмы, основанные на принципах самообучения, можно разделить на три основных группы – эвристические, корреляционные и статистические. Эвристические методы классификации основаны на разбиении диапазона значений каждого признака на заданное число градаций и в большинстве своем сводятся к расчету комплексного параметра, который является линейной комбинацией соответствующего номера интервала градации по совокупности анализируемых признаков в каждой точке наблюдений. Существенным недостатком эвристических методов является то обстоятельство, что они строятся в предположении независимости отдельных признаков между собой. Однако, наличие отдельных недостатков алгоритмов классификации не уменьшает их значимости в обработке геолого-геофизических наблюдений.

Рассматриваемые способы классификации многопризнаковых геофизических наблюдений относятся к числу эвристических и направлены на решение задачи выделения в многомерном пространстве компактных групп точек. В прикладных задачах автоматической классификации (при отсутствии эталонных объектов) эвристические алгоритмы стали применяться одними из первых и до сих пор сохраняют большое значение благодаря наглядности полученных результатов и, как правило, простоте реализации.

Разделение рассматриваемой совокупности признаков на однородные (в смысле вектора среднего) группы называется классификацией. При этом термин “классификация” используют, в зависимости от контекста, для обозначения, как самого процесса разделения, так и его результата. Это понятие тесно связано с такими терминами, как группировка, типологизация, систематизация, дискриминация, кластеризация, и является одним из основополагающих в практической и научной деятельности человека.

В общей постановке задачи проблема классификации объектов заключается в том, чтобы всю анализируемую совокупность признаков, представленную в виде матрицы, разбить на сравнительно небольшое число однородных, в определенном смысле, групп или классов. Понятие однородности основано на предположении, что геометрическая близость двух или нескольких объектов означает близость их “физических” состояний, их сходство.

В общем случае понятие однородности объектов определяется заданием правила вычисления величины r_ij . характеризующей расстояние 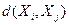между объектами Х_i и Х_j из исследуемой совокупности. Если задана функция 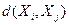. то близкие в смысле этой метрики объекты считаются однородными, принадлежащими к одному классу. Естественно, при этом необходимо сопоставление 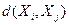с некоторым пороговым значением, определяемым в каждом конкретном случае по-своему.