Спектры стационарного случайного процесса.

Стационарный случайный процесс полностью описывается его автокорреляционной функцией, поэтому спектр случайного процесса определяется спектром АКФ. Спектр АКФ показывает, какого рода колебания (гармоники) преобладают в случайном процессе и какова его внутренняя структура. Отличие от спектров детерминированных сигналов состоит в том, что для случайного процесса амплитуды гармоник являются случайными величинами, а сам спектр случайного процесса описывает распределение дисперсий по различным гармоникам (частотам). К вычислению спектра случайного процесса можно подходить в зависимости от того, каким образом задана АКФ: в виде дискретно заданного сигнала, непрерывного периодического или непрерывного апериодического сигналов.

Поскольку АКФ – четная функция, то при анализе Фурье учитываются лишь четные (косинусные) гармоники. В зависимости от способа задания АКФ получаем спектры для АКФ в виде дискретно заданного сигнала :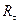

для АКФ в виде непрерывного периодического сигнала :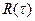

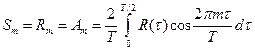
Для АКФ в виде непрерывного апериодического сигнала :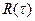

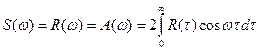(5.16).

Поскольку нечетные гармоники для спектра АКФ отсутствуют, то приведенные выражения совпадают с энергетическими спектрами. Очевидно, что обратное преобразование Фурье для АКФ симметрично прямому. Так, для (5.16) получаем: 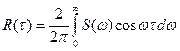(5.17).

Выражение (5.16) используется для расчета спектров наиболее распространенных АКФ в аналитическом виде:

1) АКФ «белого» шума, заданной в виде дельта-функции, т.е.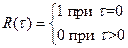

Спектр АКФ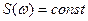

2) АКФ «треугольного» типа ; .

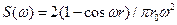3) АКФ «марковского» типа ; ;

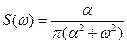4) АКФ «гауссовского» типа ; ;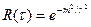

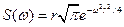5) АКФ затухающей по экспоненте косинусоиды .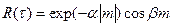

.

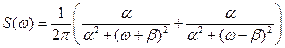АКФ гауссовского типа представляет модель гравитационных аномалий, АКФ затухающей по экспоненте косинусоиды – модель сейсмического импульса (a - определяет затухание; b - видимый период.