Вероятность случайного события

Предметом теории вероятностей является анализ закономерностей в случайных явлениях. Одной из важнейших сфер приложения теории вероятностей является психология. Практическое значение вероятностных методов состоит в том, что они позволяют по известным характеристикам простых случайных явлений прогнозировать характеристики более сложных явлений.

Пространством элементарных событий называют множество Ω взаимоисключающих исходов эксперимента такое, что каждый интересующий результат эксперимента может быть однозначно описан с помощью элементов этого множества. Элементы множества Ω называются элементарными событиями и обозначаются ω: Ω= 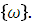Элементарныесобытия нельзя разложить на составляющие их события.

Событиемназывается исход испытания. Это понятие явля­ется первичным в теории вероятностей. События обозначаются большими латинскими буквами А, В, С, … . А, В, С, 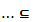Ω. Любое событие А из пространства Ω можно составить из элементарных событий.

Среди событий отличают достоверное и невозможное собы­тия. Достоверное событие— это такое событие Ω, которое все­гда происходит. Невозможное событие ? — это со­бытие, которое не может произойти.

Примеры событий: А – выпадение орла при бросании монеты, В – выигрыш в лотерею, С – реакция испытуемого на раздражитель и т.д.

Два события называются совместными в данном опыте, если появление одного из них не исключает появление другого в данном опыте. Два события называются несовместными в данном опыте, если они одновременно не могут произойти.

Несколько событий образуют полную группу, если в результате испытаний обязательно произойдет хотя бы одно из них.

Примеры:

__________________________________________________________________________________

В опыте с бросанием игральной кости (кубика) элементарны­ми событиями являются выпадения чисел 1, 2, 3, 4, 5, 6. Они образуют полную группу. В этом же опыте событиями являются выпадения четного или нечетного числа.

Совместными событиями в этом опыте будут выпадение четного числа и числа, делящегося на 3 (выпадение числа 6 фиксирует появление того и другого события).

Несовместными событиями здесь будут выпадение числа 5 и четного числа.

__________________________________________________________________

Если имеем дело со случайными событиями, то невозмож­но предсказать заранее исход того или иного опыта. Однако при ис­следовании большого количества одинаковых испытаний обна­руживаются определенные закономерности, которые можно опи­сать, используя понятие вероятности.

Под вероятностью события понимается некоторая числовая характеристика возможности наступления этого события. Суще­ствуют различные подходы к определению вероятности.