Классическое определение вероятности. Классической схемой, или схемой случаев, называется испытание, при котором число элементарных исходов конечно
Классической схемой, или схемой случаев, называется испытание, при котором число элементарных исходов конечно, и все из них равновозможны.
Случай ω называется благоприятным некоторому событию А, если его появление влечет наступление события А (т.е. ω входит в число элементов, составляющих А). Например, при бросании игральной кости возможны шесть случаев, при этом событию А – появлению нечетного числа очков – благоприятны лишь три случая: выпадение 1, 3, 5 и неблагоприятны остальные три.
Классической вероятностьюсобытия А называется отношение числа т случаев, благоприятных событию А, к числу п всех случаев:
P(A)=  .
.
Из определения следуют свойства вероятности:
1. Значение вероятности заключено между нулем и единицей:
0 < Р(А) < 1;
2. Вероятность невозможного события равна нулю:
Р(?) = 0;
3. Вероятность достоверного события равна единице:
P(Ω) = 1.
Пусть пространство Ω состоит из п элементарных событий ω1, ω2, . . . ωn. Тогда для каждого ωi благоприятным исходом будет только само ωi и для него т = 1. Поэтому
P (ωi) =  =
=  .
.
Таким образом, если в классической схеме пространство Ω состоит из п элементарных равновозможных событий, то вероятность каждого из них равна 1/ п.
Примеры:
_______________________________________________________________________ __
1. В опыте с бросанием игральной кости число всех исходов п равно 6 и все они равновозможны. Пусть событие А означает появление нечетного числа. Тогда для этого события благоприятными исходами будут появления чисел 1, 3, 5. Их количество т равно 3. Поэтому вероятность события А равна Р(А)===  .
.
2. В книге 250 страниц. Какова вероятность того, что мы откроем книгу на странице с номером, кратным 10?
Пусть событие А: «Номер открытой страницы есть число, кратное 10».Согласно классическому определению вероятности, Р(А)=  , где п — число всех возможных случаев, т — число случаев, благоприятных событию. Число п всех равновозможных случаев, образующих полную группу, равно 250. Найдем число случаев, благоприятных событию, т.е. число страниц с номером, кратным 10. Его можно вычислить, пользуясь тем, что номер нужной страницы имеет вид 10m , где m – натуральное число, причем 0≤ 10m ≤250 . Откуда находим m ≤
, где п — число всех возможных случаев, т — число случаев, благоприятных событию. Число п всех равновозможных случаев, образующих полную группу, равно 250. Найдем число случаев, благоприятных событию, т.е. число страниц с номером, кратным 10. Его можно вычислить, пользуясь тем, что номер нужной страницы имеет вид 10m , где m – натуральное число, причем 0≤ 10m ≤250 . Откуда находим m ≤  =25. Подставив полученные числа в формулу классического определения вероятности, получим:
=25. Подставив полученные числа в формулу классического определения вероятности, получим:
Р(А)=  =
= 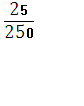 =
=  0,1.
0,1.
_____________________________________________________________________
Дата добавления: 2016-01-16; просмотров: 656;
