Условная вероятность и теоремы умножения

Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет. Вероятность события А, вычисленная при условии, чтопроизошло событие B, называется условной вероятно­стьюсобытия А и обозначается Р(А/В) (или Р_B(А)), говорят: «вероятность события А при условии В».

Условная вероятность Р(А/B) определяется формулой (при Р(В)>0)

P(A/B)= .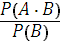

Пример:

______________________________________________________________________________________

В рассмотренном выше примере 2 Р(А ^. В) = 1/5, Р(В) = 1/2, по­этому условная вероятность равна

P(A/B) = = .

Эту же вероятность можно найти непосредственно по опре­делению. В состав события В входят 5 чисел, только 2 из чисел, входящих в А, входят также и в B. По классической формуле вероятности

P(A/B) = .

_______________________________________________________________

События А и В называются независимыми, если Р(А/B)=Р(А), т.е. вероятность события А не зависит от того, произошло ли событие В.

Как следствие рассмотренной формулы условной вероятности можно рассмотреть теоремы умножения вероятностей:

ü Вероятность произведения двух событий равна произведению одного из них на условную вероятность другого при условии, что первое произошло:

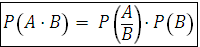, P(B) > 0 или

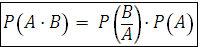, P(A) > 0

ü Вероятность произведения двух независимых событий равна произведению их вероятностей:

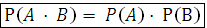
Часто последнее соотношение служит определением независимо­сти событий, так что события называются независимыми, если вероятность их произведения равна произведению вероятностей.

Примеры:________________________________________________________________________

1. Пусть события А и В несовместны и Р(А) ≠ 0, Р(В) ≠ 0. Значит, Р(А) ^.Р(В) ≠ 0. Найдем Р(А ^. В) = Р(?) = 0 . Поэтому Р(А ^. В) ≠ Р(А) ^.Р(В). Это означает, что несовместные события А и B зависимы.

2. Пусть событие А влечет за собой событие B, т.е. А Ì В, и Р(В) ≠ 1. Тогда А ^. В = А, и Р(А ^. В) = Р(А). Поэтому Р(А ^. В) ≠ Р(А) ^.Р(В). Это означает, что если А Ì В, то события А и В – зависимы.

________________________________________________________________