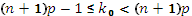Формула полной вероятности и формула Байеса
Рассмотрим п попарно несовместных событий H1, H2, . . . , Hn. Они образуют полную группу событий, если они попарно несовместны, а их сумма является достоверным событием, т.е.
Hi . Нj = ? при i ≠ j и H1 +H2 + . . . + Нn = Ω.
Такие события называются гипотезами.
Простейшим примером полной группы событий является произвольное событие А и его дополнение Ā. По теореме сложения вероятностей, для полной группы событий справедливо равенство
Р(Н1) + Р(Н2) + . . .+ Р(Нп) =1.
Примеры:
__________________________ _____________________________
1. Пусть Ω = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Рассмотрим события H1 = {2, 4, 6, 8, 10}, H2 = {1, 3}, H3 = {5, 7, 9}. Они попарно несовместны, а их сумма является достоверным событием Ω. Значит, Н1, H2, H3 составляют полную группу событий. Для них Р(Н1) = 5/10, Р(H2) = 2/10, Р(Н3) = 3/10, т.е. сумма их вероятностей равна 1.
2. В лесу растут деревья, среди которых 60 % берез, 10 % елей, и 30 % сосен. [3, c. 16]. Случайным образом выбирается для замера одно из деревьев. Обозначим гипотезы: Н1 – «выбранное дерево – береза», H2 – «выбранное дерево – ель», H3 – «выбранное дерево – сосна». Тогда события H1, H2, H3 – попарно несовместны, Р(Н1) = 0,6, Р(Н2) = 0,1, Р(Н3) = 0,3. Значит, гипотезы H1, H2, H3 составляют полную группу событий. Сумма их вероятностей равна 1.
_______________________________________________________________________________
Пусть события H1, H2, . . ., Нп образуют полную группу событий. Тогда для любого события А имеет место формула полной вероятности:
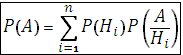
Пример:
_______________________________________________________________________
Рассмотрим предыдущий пример 2. Пусть при замере диаметра деревьев он оказался больше 15 см для 30 % берез, 40 % елей и 70 % сосен. Введем событие А – «диаметр случайно выбранного дерева больше 15 см». Найдем вероятность этого события. По условию примера, условные вероятности события А равны: Р(А/H1) = 0,3, P(А/H2) = 0,4, Р (А/H3) = 0,7. Тогда по формуле полной вероятности имеем:
Р(А) = P(H1)P (А/H1) + Р(Н2)Р(А/H2) + Р(Н3)Р(А/H3) = 0,6 . 0,3 + 0,1 . 0,4 + 0,3 . 0,7 = 0,43.
___________________________________________________________________
В формулу полной вероятности входят вероятности Р(Н1), Р(Н2), . . ., Р(Нn), которые называются априорными. Это вероятности гипотез Нi , вычисленные до опыта (a priori). Если событие А наступило, то эти вероятности изменяются. Это будут апостериорные условные вероятности, вычисленные после опыта (a posteriori) P(H1/A), PA(H2/A), . . . , PA(Hn/A). Они могут быть найдены по формуле Байеса:
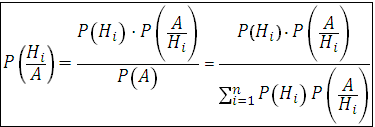
Пример:___________________________________________________________________________
Пусть в условиях предыдущего примерадиаметр случайно выбранного дерева оказался больше на 15 см, т.е. событие А наступило. Найти вероятность того, что измеренное дерево – береза. По формуле Байеса имеем:
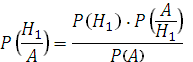 =
= 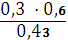 = 0,42.
= 0,42.
______________________________________________________________
Формула Бернулли
Опыты называются независимыми, если вероятность исхода каждого опыта не зависит от того, какие исходы имели другие опыты. Пусть проводятся n независимых опытов, в результате которых может появиться событие A с вероятностью p и не появиться с вероятностью q, причем p+q = 1. Такая схема называется схемой Бернулли.
Пусть X – число появлений события А в n испытаниях Бернулли. Тогда вероятность того, что в серии из п независимых испытаний событие А появится ровно 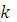 раз (Х=k) вычисляется по формуле Бернулли:
раз (Х=k) вычисляется по формуле Бернулли:
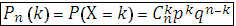
Пример:
_________________________________________________________ _
Вероятность попадания в мишень для конкретного стрелка равна 0,7. Какова вероятность того, что из 10 выстрелов будет 4 попадания в мишень?
Воспользуемся формулой Бернулли  при k = 4, n = 10, p = 0,7. Искомая вероятность равна
при k = 4, n = 10, p = 0,7. Искомая вероятность равна  = 0,0367.
= 0,0367.
________________________________________________________________
|
Пример:
________________________________________________________ ___
Всхожесть семян некоторого растения имеет вероятность 0,8. Найти наиболее вероятное число проросших семян из 7 посеянных.
По формуле 8 ∙ 0,8-1 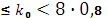 , поэтому
, поэтому 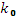 = 6.
= 6.
______________________________________________________________
 5.7. Формула Пуассона
5.7. Формула Пуассона
Если в схеме испытаний Бернулли число испытаний n велико, вероятность p события A в одном испытании мала, а произведение λ = np не превосходит 20, то вероятность 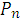 (m) того, что событие A появится ровно в m испытаниях, находится по приближенной формуле Пуассона:
(m) того, что событие A появится ровно в m испытаниях, находится по приближенной формуле Пуассона:
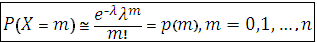
Значения 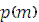 имеются в таблицах значений функции Пуассона.
имеются в таблицах значений функции Пуассона.
Пример:
______________________________________________________ __
В ходе проверки случайным образом отбирается 10 счетов. Найти вероятность того, что обнаружится один счет с ошибкой, если в среднем 3% счетов содержат ошибки.
Для решения задачи используем формулу Пуассона, в которой n = 10, p=0,03, λ = np = 0,3. Имеем
 По таблицам значений функции Пуассона находим 0,2223.
По таблицам значений функции Пуассона находим 0,2223.
5.8. Локальная формула Муавра – Лапласа
Если число испытаний n достаточно велико, то вероятность появления события A ровно m раз в схеме из n испытаний Бернулли можно вычислять по приближенной формуле Муавра – Лапласа:
где
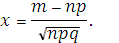
Причем 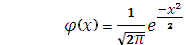 – малая функция Лапласа (функция Гаусса), значения которой имеются в соответствующих таблицах.
– малая функция Лапласа (функция Гаусса), значения которой имеются в соответствующих таблицах.
Пример: _________________________________________________________ _
Вероятность найти белый гриб среди прочих равна 0,25. Какова вероятность того, что среди 70 грибов белых будет 20?
По формуле Муавра – Лапласа при n=70, m=20 имеем:
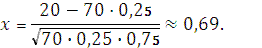
По таблицам определяем значениеТогда
.
 ______________________________________________________________
______________________________________________________________
5.9. Интегральная формула Муавра – Лапласа
Для того, чтобы определить вероятность попадания числа m (появления события A в схеме Бернулли при большом числе испытаний n) в заданный промежуток [а,в]: 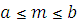 , можно использовать интегральную формулу Муавра – Лапласа:
, можно использовать интегральную формулу Муавра – Лапласа:
| |
где
– функция Лапласа, значения которой находятся по таблицам.
Для относительной частоты (частости) m/n появления события A в n испытаниях Бернулли справедлива приближенная формула
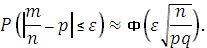
Для числа m появлений события A справедлива приближенная формула
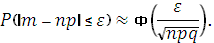
Примеры:
______________________________________________________
1. В партии из 768 арбузов каждый арбуз оказывается неспелым с вероятностью q = 0,25. Найти вероятность того, что количество спелых арбузов будет находиться в пределах от 560 до 600.
Из условия задачи имеем n=768 испытаний Бернулли с вероятностью найти зрелый арбуз, равной р=0,75. Если m – число удачных выборов, то требуется найти вероятность 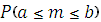 , где a = 560, b = 600.
, где a = 560, b = 600.
Поскольку
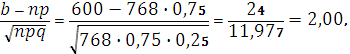
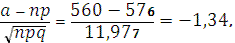
то по интегральной формуле Муавра – Лапласа получим:
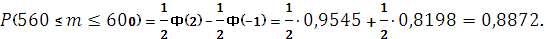
2. Сколько нужно произвести бросаний монеты, чтобы с вероятностью 0,99 можно было утверждать, что относительная частота выпадения герба отличается от 0,5 по модулю не более чем на 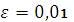 ?
?
По формуле 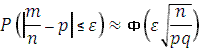 , в которой
, в которой 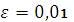 , имеем:
, имеем:
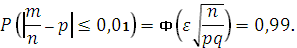
По таблицам значений функции Лапласа находим, что
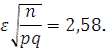
Откуда выражаем п и, подставляя p=0,5; q=0,5, получим:
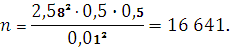
________________________________________________________________
Дата добавления: 2016-01-16; просмотров: 3531;