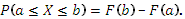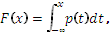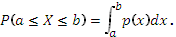Непрерывные случайные величины. Плотность распределения
Непрерывной называется случайная величина X, если ее функция распределения непрерывна.
Распределением непрерывной случайной величины называется совокупность вероятностей P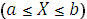 
для любых действительных чисел 
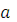и 
.
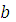Распределение непрерывной случайной величины однозначно определяется ее функцией распределения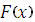 
, так как
|
Если Х – непрерывная случайная величина, то вероятность того, что она примет одно, заданное определенное значение α, равна нулю.
Р(Х=α) = 0
Все свойства функции распределения дискретных случайных величин выполняются и для функций распределения непрерывных случайных величин.
Плотностью распределения вероятностей случайной величины Х в точке х называется предел отношения вероятности попадания значений этой величины в интервал (х; х+∆х) к длине ∆х отрезка [х; х+∆х], при стремлении ∆х к нулю:
р(х) =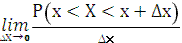 
.
График функции р(х) (плотности распределения) называется кривой распределения.
Справедливо следующее равенство:
|
Если случайная величина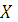 
имеет плотность, то она является непрерывной случайной величиной.
Плотность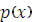 
однозначно определяет распределение случайной величины, поскольку вероятность попадания значений случайной величины Х в интервал (а; в) равна определенному интегралу от плотности распределения :
|
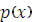Плотность распределения обладает следующими свойствами:
1. Плотность распределения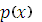 
– неотрицательная функция, т.е.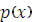 
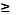0.
2. Из определения плотности следует, что, так что, если 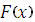дифференцируема, то она имеет плотность.
3. 
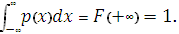
Если все возможные значения принадлежат отрезку [а; в], то
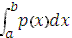= 1,
так как 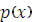= 0 вне этого отрезка.
Пример:
__________________________________________________________________________________
Плотность вероятности случайной величины Х задана функцией
= 
.
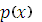Найти вероятность того, что в результате испытания величина Х примет значение из интервала (1; 2).
______________________________________________________________
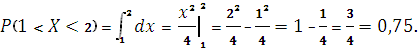
Дата добавления: 2016-01-16; просмотров: 842;