Основные теоремы теории вероятностей
Теоремы сложения
ü Вероятность суммы несовместных событий A и B равна сумме их вероятностей:
(*)
ü Вероятность суммы совместных событий A и B равна сумме их вероятностей без вероятности их совместного появления:
(**)
ü Сумма вероятностей противоположных событий равна единице:

Примеры:________________________________________________________________________
1. Пусть пространством событий является множество чисел Ω = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, в котором все числа – элементарные события – равновозможны, вероятность каждого из них равна 1/10. Пусть A = {1,3, 5, 7}, В= {2, 4, 6}, тогда A и B несовместны и А + В = {1, 2, 3, 4, 5, 6, 7}. Найдем
Р(А) =  =
=  , Р(В) =
, Р(В) =  , Р(А+В)=
, Р(А+В)=  .
.
Проверим результат вычисления по формуле (*):
Р(А+В) =  +
+  =
=  .
.
2. Пусть пространством событий является множество чисел Ω = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, в котором все числа – элементарные события – равновозможны, вероятность каждого из них равна 1/10. Пусть А = {2, 3, 5, 7, 10}, В = {2, 5, 6, 8, 9}, тогда А . В = {2, 5}, А + В = { 2, 3, 5, 6, 7, 8, 9, 10},
Р(А) =  =
=  , Р(В) =
, Р(В) =  =
=  , Р(А·В) =
, Р(А·В) =  =
=  , Р(А+В) =
, Р(А+В) =  =
=  .
.
что соответствует формуле (**):
Р(А+В) =  +
+  –
–  = 1 –
= 1 –  =
=  .
.
3. Пусть в группе из 27 туристов 17 человек владеют английским языком, 6 – французским, а 2 – обоими языками. Найти вероятность того, что случайно выбранный из группы турист владеет по крайней мере одним из этих языков [3, с. 13].
Введем событие: А – «выбранный турист владеет английским», В – «выбранный турист владеет французским». Тогда событие А + В означает, что турист владеет хотя бы одним из этих языков. По условию задачи
Р(А) = 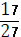 , Р(В) =
, Р(В) =  , Р(АВ) =
, Р(АВ) =  .
.
по формуле (**)имеем:
Р(А+В) = Р(А) + Р(В) – Р(АВ) = 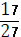 +
+  -
-  =
= 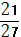 =
=  .
.
____________________________________________________________
Дата добавления: 2016-01-16; просмотров: 1123;
