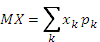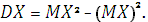Математическое ожидание и дисперсия дискретной случайной величины

Математическое ожидание MX дискретной случайной величины X определяется формулой

и имеет смысл среднего значения случайной величины. Если число значений случайной величины конечно и равно n, а вероятности 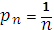, то MX совпадает с обычным средним значением величин :

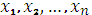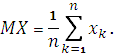
Математическое ожидание обладает следующими свойствами:

1. MC = C, где C = const;

2. M (CX) = C∙MX, где C = const;

3. M(X 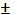Y) = MX 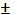MY, для любых X и Y;

4. M (X∙Y) = MX∙MY, если X и Y независимы.

Для оценки степени рассеивания значений случайной величины вокруг ее среднего значения вводится понятие дисперсии.

Дисперсией (DX) называется математическое ожидание квадрата разности (X – MX):

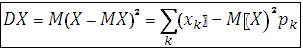
Для вычисления дисперсии обычно используют более удобную формулу

Свойства дисперсии: σX = ,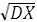

1. DC = 0, где C = const;

2. D (CX) = 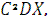где C = const;

3. D (X 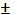Y) = DX+DY, если X и Y независимы.

Средним квадратическим отклонением называется величина

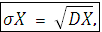
которая также является мерой рассеивания случайной величины X.

Пример:

__________________________________________________________________________________

Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X для примера о всхожести семян из п. 5.10.

По формуле математического ожидания имеем:

MX = 0∙0,01024+1∙0,0768+2+0,2304+3∙0,3456+4∙0,2592+5∙0,07776=3.

Для вычисления дисперсии сначала найдем 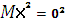∙0,01024+ 0,0768+ ∙0,2304+ ∙0,3456+ ∙0,2592+ ∙0,07776=10,2. По формуле дисперсии находим DX = 10,2-3²=1,2. Тогда σX = 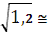1,905