Нахождение наибольшего и наименьшего значений непрерывной функции на отрезке
Для того чтобы найти наибольшее и наименьшее значения непрерывной функции на отрезке 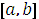 , необходимо:
, необходимо:
1. Найти критические точки на этом отрезке.
2. Подсчитать значения в этих точках и на концах отрезка.
3. Выбрать из найденных значений наибольшее и наименьшее.
Примеры:____________________________________________________
1. Исследуем на экстремум следующие функции:  ,
, 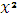 , x, 1-
, x, 1-  . Решение представим в виде таблицы (табл. 4.5).
. Решение представим в виде таблицы (табл. 4.5).
Таблица 4.5
| f(x) | 
| 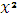
| x | 1- 
|
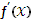
| 3 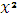
| 2x | 1 | 
|
Критическая точка 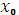
| Нет | |||
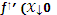 ) )
| Не существует | |||
Знак 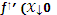 )
(лев., прав.) )
(лев., прав.)
|   + + + +
|   – + – +
|   + + + +
|   + – + –
|
| Экстремум | Нет | min | Нет | max |
| График |   
|   
|   
|    
|
2. Найти наибольшее и наименьшее значения функции y =  -3x+1 на отрезке
-3x+1 на отрезке 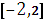 .
.
 (x) =3
(x) =3 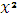 -3 = 0
-3 = 0 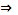
 =
= 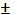 1.
1.
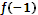 = 3, ?
= 3, ?  = -1,
= -1,  = -1,
= -1, 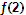 = 3.
= 3.
Итак, 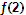 =
= 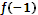 = 3 – наибольшее, а
= 3 – наибольшее, а 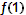 =
=  = -1 – наименьшее значение.
= -1 – наименьшее значение.
________________________________________________________________
4.9. Неопределённый интеграл
Первообразная и неопределённый интеграл
Обратной операцией для дифференцирования функции является нахождение её первообразной.
Первообразной для функции y= 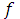 (x) называется такая функция F(x),что F’(x)=f(x) для всех х из области определения f(x).
(x) называется такая функция F(x),что F’(x)=f(x) для всех х из области определения f(x).
Пример:
_______________________________________________________________
Для функции у=3х2 первообразной является функция F(x)=x3, а также функция F1(x)=x3+5.
_____________________________________________________________
Как видно из примера, первообразная не определяется однозначно.
Если две функции F1(x) и F2(x) являются первообразными для одной и той же функции 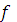 (x), то их разность F1(x)-F2(x) = C = const (является постоянной функцией). Отсюда следует, что множество всех первообразных для данной функции
(x), то их разность F1(x)-F2(x) = C = const (является постоянной функцией). Отсюда следует, что множество всех первообразных для данной функции 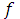 (x) состоит из функций, отличающихся друг от друга на постоянную.
(x) состоит из функций, отличающихся друг от друга на постоянную.
Неопределённым интегралом от функции 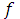 (x) называется совокупность всех первообразных этой функции.
(x) называется совокупность всех первообразных этой функции.
Неопределённый интеграл от функции 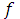 (x) обозначается
(x) обозначается
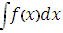 .
.
Если функция F(x) является одной из первообразных для 
 =F(x)+C.
=F(x)+C.
Функция 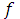 (x) называется подынтегральной функцией, а выражение
(x) называется подынтегральной функцией, а выражение  подынтегральным выражением
подынтегральным выражением 
Пример:
__________________________________________________________________________________
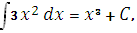
где С – произвольная постоянная.
________________________________________________________________
Достаточным условием для существования неопределённого интеграла от функции 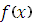 является непрерывность этой функции.
является непрерывность этой функции.
Свойства неопределённого интеграла
1. Производная неопределённого интеграла (т.е. каждой его составляющей первообразной функции) равна подынтегральной функции:
(
2. Дифференциал от неопределённого интеграла (т.е. от каждой его составляющей первообразной функции) равен подынтегральному выражению:

3. Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
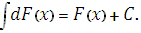
4. Постоянный множитель можно выносить из-под знака неопределённого интеграла:

5. Неопределённый интеграл от алгебраической суммы функции равен алгебраической сумме неопределённых интегралов от слагаемых:

6. Если 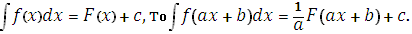
Таблица основных интегралов
1. 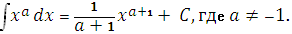
2. 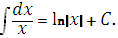
3. 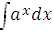 =
= 
4. 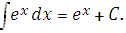
5. 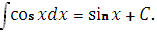
6. 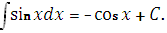
7. 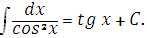
8. 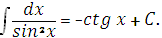
9. 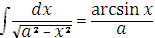 + C.
+ C.
10.  arctg
arctg  + C.
+ C.
11. 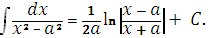
12.
Примеры:
_________________________________________________________________________________
1. 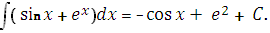
2. 
3. 
___________________________________________________________
4.10. Определённый интеграл
Пусть функция y = f(x) определена на отрезке [a,b]. Разобьём отрезок [a,b] на n частей точками 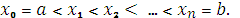 На каждом из полученных отрезков [
На каждом из полученных отрезков [  (i=1,2,…, n) возьмем некоторую точку
(i=1,2,…, n) возьмем некоторую точку
Интегральной суммой функции y = f(x) на отрезке [a,b] называется сумма
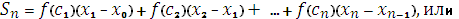
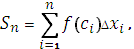
|
где 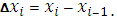
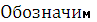 наибольшую из длин
наибольшую из длин 
Определённым интегралом функции y = f(x) на отрезке [a,b], который обозначается
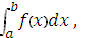 называется предел интегральных сумм
называется предел интегральных сумм
 (*)
(*)
Таким образом,
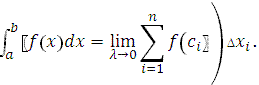
|
Интегрируемой называется функция, для которой существует предел, обозначенный (*). Из условия 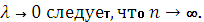 Числа a и bназываются пределами интегрирования. Функция f(x) носит название подынтегральной функции.
Числа a и bназываются пределами интегрирования. Функция f(x) носит название подынтегральной функции.
Если функция y=f(x) непрерывна на отрезке [a,b], то определённый интеграл 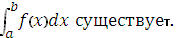
|
Пример:
______________________________________________________________
Пусть y=A – постоянная функция на отрезке [a,b]. Тогда интегральная сумма имеет вид:

Она зависит от способа разбиения отрезка на части и
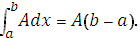
 Полученное число равно площади заштрихованного прямоугольника на рис. 4.10.
Полученное число равно площади заштрихованного прямоугольника на рис. 4.10.
у
 A
A 
















 0 a b x
0 a b x
Рис 4.10.
________________________________________________________________
Свойства определённого интеграла
1. 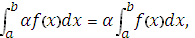 где
где  - произвольное число.
- произвольное число.
2. 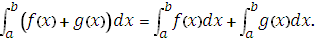
3. 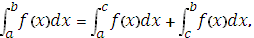 где a<c<b.
где a<c<b.
4. 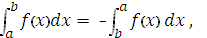 а>в
а>в
5. Если для всех x 
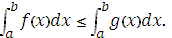
6. Для 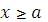 производная определённого интеграла
производная определённого интеграла
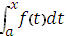
равна значению подынтегральной функции в точке 
7. Теорема о среднем: если функция 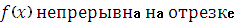 [a, b], то существует точка c
[a, b], то существует точка c 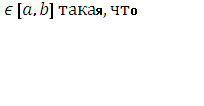
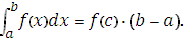
8.Оценка модуля интеграла:если  [a,b], то
[a,b], то 
9. Формула Ньютона – Лейбница (связывает неопределённый и определённый интегралы):если функция  непрерывна на отрезке [a, b], а функция
непрерывна на отрезке [a, b], а функция 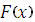 - какая-либо её первообразная ( т.е.
- какая-либо её первообразная ( т.е. 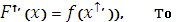
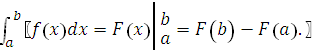
Пример:
__________________________________________________________________________________

________________________________________________________________
Дата добавления: 2016-01-16; просмотров: 1241;
