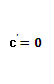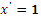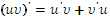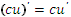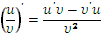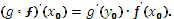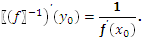Правила дифференцирования

1. Производная постоянной равна нулю, т.е

2. Производная аргумента равна 1, т.е.

В следующих правилах будем полагать, что u=u(x) и υ=υ(x) – дифференцируемые функции.

3. Производная алгебраической суммы функций равна сумме производных этих функций, т.е.

4. Производная произведения двух функций равна

5. Постоянный множитель можно выносить за знак производной:

6. Производная частного двух функций вычисляется по формуле

(при условии, что υ≠0).

7. Производная сложной функции.

Пусть заданы функции y=?(x) и z=g(y), для которых определена сложная функция z=g(?(x)). Тогда, если функция y=?(x) дифференцируема в точке 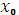, а функция z=g(y) дифференцируема в точке 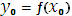, то производная сложной функции z=(g ◦ ?)(x) в точке 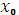вычисляется по формуле

1. Производная обратной функции

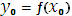Если для функции y=?(x) существует обратная функция x= и производная существует, то производная обратной функции в точке вычисляется по формуле

Таблица производных

Все основные элементарные функции являются дифференцируемыми и имеют производные, приведенные в табл. 4.4.

Таблица 4.4

Функция y	Производная	Функция y	Производная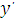
c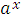
x
u+υ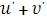
uυ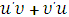
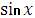
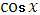
cu
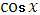
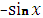
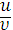
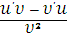
		tg x
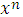
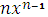
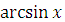
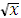
		arccos x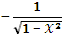
		arctg x
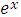
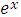
		g(f(x))