Элементарные функции
В таблице 4.2 приведен перечень известных из школьного курса функций и их графиков. Эти функции называются основными элементарными функциями.
Элементарными функциями называются функции, которые можно получить из основных элементарных функций (перечисленных в таблице) с помощью алгебраических операций и композиций функций.
Примеры:
__________________________________________________________________________________
1. Функция
у = 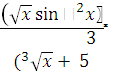 +
+ 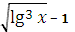
является элементарной, так как она получена с помощью операций сложения, вычитания, умножения, деления и образования сложной функции.
2. Функция у = |x| (рис. 4.4)  является примером неэлементарной функции
является примером неэлементарной функции
у

 y = |x|
y = |x|

х
Рис. 4.4
________________________________________________________________
Таблица 4.2
| Аналитическое задание | Область определения Х | Область значений Y | График |
1. Степенная функция
у = xⁿ ,
n 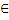 N N
 у = x⁻ⁿ ,
n
у = x⁻ⁿ ,
n 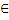 N N
 y =
y = 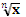 ,
n ,
n 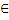 N,
n N,
n 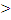 1 1
| (-  , + , +  )
(- )
(-  , 0) , 0) 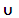 (-
(- 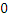 , + , +  )
(- )
(-  , + , +  ),
если n нечетно; ),
если n нечетно;
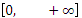 , если n четно , если n четно
| (-  , + , +  ),
Если n нечетно; , если n четно
(- ),
Если n нечетно; , если n четно
(-  , 0) , 0) 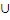 (-
(- 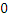 , + , +  ), если n нечетно; ), если n нечетно; 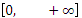 , если n четно
(- , если n четно
(-  , + , +  ),
если n нечетно; ),
если n нечетно;
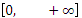 , если n четно , если n четно
|
0 1 х 0 1 х
у =
|
2.Показательная функция
у = 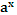 ,
а ,
а 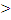 0,
а 0,
а 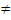 1 1
| (-  , + , +  ) )
| 
| 
  y
y = y
y = 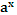 0
0 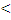 a a 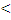 1
1 a 1
1 a 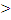 1 1
 0 1 x 0 1 x
|
| Аналитическое задание | Область определения Х | Область значений Y | График |
3.Логарифмическая функция
y = 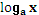 ₁
a ₁
a 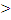 0,
a 0,
a 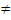 1 1
| ( 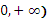
| (-  , + , +  ) )
|
  Y Y
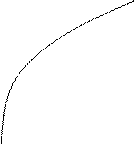 a > 1
y =
a > 1
y = 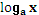
  0 1 x
0 < a < 1
0 1 x
0 < a < 1
|
4.Тригонометрические функции
y = sin x
 У = сos x У = сos x
| (-  , + , +  )
(- )
(-  , + , +  ) )
| [-1,1] [-1,1] |  у
у
   
 0 0
 -2П -П П/2 П 2П х
-1 -2П -П П/2 П 2П х
-1
 y y
-п -
-1
|
| y = tg x | (-  + Пn, + Пn,  + Пn),
N + Пn),
N 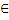 Z Z
| (-  , + , +  ) )
|        y y
 -п -
-п -  0 0  П x П x
|
Предел функции
Понятие предела является математическим выражением факта одновременного стремления двух связанных величин к некоторым значениям.
Примеры:
__________________________________________________________________________________
ü если вы читаете литературу со скоростью 60 страниц в час, то при стремлении времени чтения к двум часам числе прочитанных страниц будет стремиться к 120;
ü если количество рекламных вставок равно 30 в час, то при приближении времени просмотра телепередачи к трем часам число реклам будет приближаться к 90;
ü вы усиленно работаете над своим характером, чтобы быть похожим на Васю, который нравится Марине, а она нравится вам; тогда, если вы станете похожим на Васю, степень благосклонности Марины к вам будет почти такой же, как и к Васе [1, с. 112].
_______________________________________________________________
Понятие предела является одним из основных в математике. Рассмотрим любую функцию, например у = x3; зададим любое значение х, к примеру, х = 2. Возьмём последовательность чисел x, близких к числу 2, и вычислим значения уi = хi3. Один из вариантов последовательностей чисел xi и уi. приведен в табл. 4.3.
Таблица 4.3
| x | 1,96 | 1,97 | 1,98 | 1,99 | 2,01 | 2,02 | 2,03 | 2,04 | |
| y | 7,53 | 7,64 | 7,76 | 7,88 | 8,12 | 8,24 | 8,36 | 8,49 |
Приведенная в таблице последовательность чисел имеет следующую закономерность: чем меньше число х отличается от числа 2, тем меньше соответствующее значение у отличается от числа 8. Т. е. при стремлении числа х к 2 число у стремится к 8, какие бы последовательности чисел xi и уi = хi3 мы ни рассматривали.
Число А называется пределомфункции у = f(x) при стремлении х к а (или в точке х = а), если для всех значений х (х ≠ а), сколь угодно мало отличающихся от а, соответствующие значения у сколь угодно мало отличаются от А.
 | |||
 | |||

y у = f(x)


 A +ε
A +ε

 A 2ε
A 2ε
 A – ε
A – ε


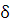
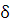
0 х₀ - 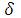 х₀ х₀ +
х₀ х₀ + 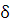 x
x
Рис. 4.5
Число А — предел функции y=f(x) при х → а, если для любого положительного числа ε можно указать такое положительное число δ, зависящее от ε, что для всех х, удовлетворяющих неравенству 0 < |х - а| <δ, имеет место неравенство |f(x) — А| < ε.
Символическая запись: lim f(x) = A
x→a
Пример:
__________________________________________________________________________________
 Предел функции у=х2 в точке х=2 равен 4. Записываем:
Предел функции у=х2 в точке х=2 равен 4. Записываем: 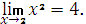
____________________________________________________________
Дата добавления: 2016-01-16; просмотров: 686;


 у у
у у
 y =
y = 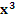
 1
1
 у = х
у = х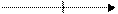



 у у
у у

 у = 1/x у =1/ х?
у = 1/x у =1/ х?

 0 1 x 0 1 x
0 1 x 0 1 x

 у у
у у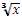 у =
у = 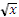



 1 х 0 1 х
1 х 0 1 х

 0
0 

