ОСНОВЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА
Понятие функции
Понятие функции было введено в гл. 1, раздел 1.3. Рассмотрим частный случай этого понятия, а именно числовые функции. Область отправления и область прибытия в данном случае — множество действительных чисел.
Функция – это соответствие (закон), согласно которому каждому значению переменной х из некоторого множества Х отвечает вполне определенное число у. Функция записывается в виде у = f(х), число х называется аргументом, а у – значением функции. Множество Х называется областью определения функции. Соответствующие значения у образуют множество значений функции.
Функции можно задавать:
а) аналитически с помощью формул;
б) таблицами;
в) графически.
Примеры:
1. Аналитический способ: у = х3 + 2; у = sin2 x.
2. Табличныйспособ: таблицы составляются по данным экспериментального изучения связи между двумя величинами, например, в результате измерения влажности воздуха в различные часы дня (табл. 4.1). В этой таблице φопределена как функция t.
Таблица 4.1
| Время (t),ч. | |||||||
| Влажность (φ), % |
3. Графический способ заключается в следующем: в прямоугольной системе координат задается некоторое множество точек М (х;у), и при этом никакие две точки не лежат на одной прямой, параллельной оси Оу. Это множество точек определяет функцию у = f(x). Абсциссы точек являются значениями аргумента, ординаты — значениями функции.
Функция называется возрастающей,если большему значению аргумента соответствует большее значение функции; функция убывающая,если большему значению аргумента соответствует меньшее значение функции. Иначе это можно записать так: функция y=?(x) называется возрастающей (убывающей) на промежутке X, если для любых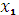 
, 
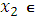X, 
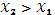, верно неравенство
?( 
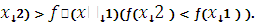
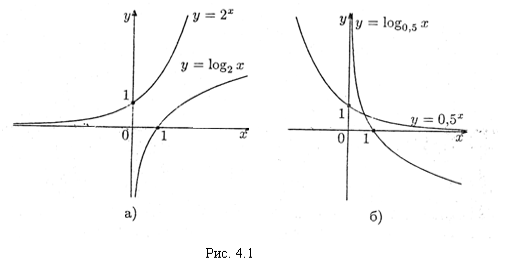
Возрастающая (рис. 4.1,а) и убывающая (рис. 4.1,б)функции называются монотонными.
Примеры:
Возрастающими являются функции:
ü площадь S квадрата, зависящая от его стороны a: S = а2;
ü численность народонаселения в городе Энске с течением времени при условии, что рождаемость выше смертности: у = 50000 • еt/32, где е ≈ 2,7;
ü путь, пройденный телом, в зависимости от времени движения:
S = t + 2t2;
Убывающими являются такие функции:
ü время проезда от Минска до Бреста по железной дороге в зависимости от скорости: t = 
;
ü число больных гриппом в городе Энске с течением времени в данный зимний период при ежедневном контроле, если прирост выздоровевших больше прироста заболевших: у = 20000 • е-t/10.
Функция четная,если у(- х) = у(х), и нечетная, если у(- х) = —у(х) для любого х из области определения функции. Например: у = cos x — четная функция, a y = sin x — нечетная (рис. 5.2). Функция у = 2x не является как четной, так и нечетной, поскольку 2-x ≠ 2x и 2-x ≠ - 2x.
Функция является пеpuoдическойс периодом Т, если для любого значения аргумента у(х + Т) = у(х), т.е. функция повторяет свои значения через данный промежуток Т. Периодическими являются, например, функции у = sin x, у = cos x (см. рис. 4.2).
Периодические функции описывают, в частности, звуковые и электромагнитные волны (сигналы).
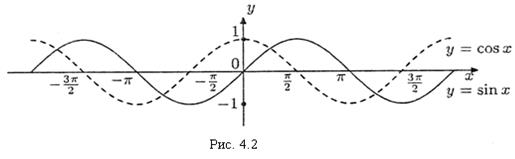
Функция ограничена, если |f(х)| ≤ М для некоторого действительного числа М > 0 и для любого значения х из области определения функции. Функции у = cos x и у = sin x — ограниченные функции, поскольку выполняется: |sin x| ≤ 1 и |cos x| ≤ 1.
Ограниченность играет важную роль и в природных явлениях, и в социальных.
Нулямифункции называются значения аргумента, обращающие функцию в нуль. Например, нулями функции у = х2 - 4 являются значения x1 = 2 и x2= - 2.
Пример:
Вид графика зависимости между стимулом и реакцией изображен на рис. 4.3.
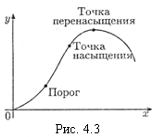
Проанализируем этот график [1, с. 109]. Рассмотренная функция возрастает до точки перенасыщения, а далее стремительно убывает. Она ограничена, поскольку изменяется от нулевого значения до максимального, определенного точкой перенасыщения. Функция непериодическая, нуль функции при х = 0.
Пусть имеют две функции у =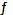 
(x) и ζ = 
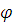(y). Тогда для тех х, для которых значения у = 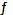(x) принадлежат области определения функции 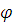(y), можно определить функцию ζ =( 
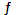(x)). Эта функция называется сложной функциейили композицией функци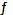й и 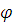и обозначается
ζ = (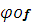 
) (x)
Пример:
Для функций у = -х? + 4, ζ = 2у – 2 их композицией будет функция ζ = 2(-х? + 4) – 2 = -2х? + 6.
________________________________________________________________
Дата добавления: 2016-01-16; просмотров: 602;