Непрерывность функций.

С пределом функции тесно связана ее непрерывность, означающая малое изменение функции при малом изменении аргумента.

Пусть функция f(х) определена при некотором значении x₀ и в некотором интервале с центром в x₀ (т.е. в окрестности х₀). Очевидно, что

при х=х₀ функция имеет значение у = f(х₀), а при х=х₀+∆х значение функции у = f(х₀+∆х). Приращение функции равно

∆у= f(х₀+∆х)- f(х₀),

Функция у=f(х) называется непрерывной в точке x₀, если она определена в самой этой точке и некоторой ее окрестности и

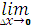∆у=0 либо иначе 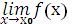= f(х₀),

Это условие непрерывности используется при вычислении пределов, а именно: если функция у = f(x) непрерывна в точке x₀, то при вычислении ее предела в этой точке нужно подставить в функцию вместо аргумен­та х значение x₀.

Примеры:

__________________________________________________________________________________

1. 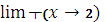е^3х+2=е⁸

2. (sinx+2x²-3cos4x)=-3

___________________________________________________________________________

Справедлива следующая теорема.

Теорема. Всякая элементарная функция непрерывна в каждой точ­ке, в которой она определена.

Если функция f(х) непрерывна в каждой точке некоторого интервала (а, b), то говорят, что функция непрерывна на этом интер­вале. Если функция f(х) непрерывна в каждой точке интервала (а, b) и непрерывна на концах интервала соответственно справа и слева, то говорят, что f(х) непрерывна на отрезке [a, b].

Непрерывность играет большую роль в природе и в обществе.

Примеры:

__________________________________________________________________________________

1. Непрерывность в природе: известно, что рост и развитие организма происходит непрерывно, испытывая малые изменения за малый промежуток вре­мени. Представьте, что было бы, например, с шестилетним ребенком, если бы вдруг однажды за один день его рост увеличился на 10 см. Это была бы катастрофа для всего организма, ведь за кратчайший срок из­менилась бы деятельность всех органов и систем.

2. Непрерывность в обществе: постепенное (непрерывное) развитие дает возможность осуществлять прогноз и корректировку, учитывая огромное множество различных факторов; при больших скачках (разрывах) в развитии возможны социально-экономические взрывы (дефолты, революции).

3. Один из важнейших вопросов психологии: можно ли повлиять на характер человека? Ответ будет положительным, если соответствую­щая работа осуществляется медленно и постепенно, а скачки, связан­ные с разрывами различных психических процессов, могут привести негативным последствиям [1, с. 120].

______________________________________________________________

Производная

Пусть функция y=?(x) определена и непрерывна в некоторой окрестности точки x. Тогда приращению ∆x независимой переменной x соответствует приращение функции ∆y=?(x+∆x)-?(x). Однако более важным для исследования свойств функции является не само приращение ∆y, а относительное приращение .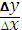

Производной функции y=?(x) в точке x называется предел относительного приращения 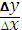при ∆x→0. Этот предел обозначается

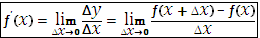
Дифференцируемой называется функция, которая имеет производную.

Дифференцированием называется операция нахождения производной.