Геометрический смысл производной

Рассмотрим график некоторой функции (рис.4.6). Касательная прямая к графику в точке (x,?(x))образует с осью Оx угол α, для которого

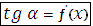
y

y=?(x)

^α

0 х х

Рис. 4.6

Физический смысл производной

Пусть S(t) – путь, пройденный материальной точкой за время t. Тогда ∆S(t)=S(t+∆t)-S(t) – участок пути, проходимый за время ∆t. Отношение 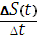есть средняя скорость на участке ∆S(t) пути, а

=

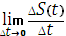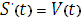
есть мгновенная скорость в точке t.

Если же 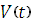скорость в точке t, то 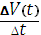есть среднее ускорение на участке времени ∆t, а

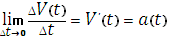
есть ускорение в момент времени t.

Таким образом, вторая производная от пути

a(t)=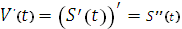

есть ускорение в момент времени t.

В общем случае, если у(t) описывает произвольный процесс, разворачивающийся во времени, то у'(t) есть скорость этого процесса. Для функции с аргументом х, не обязательно обозначающим время, отношение 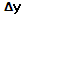– средняя скорость изменения у относительно изменения х, а у'(х) – мгновенная скорость изменения у.

Пример:

__________________________________________________________________________________

Пусть некоторый физиологический процесс описывается формулой у=4t³+5t²-3t. Найти скорость в момент времени t=2.

V(t)=y'(t)=12t²+10t-3. y'(2)=12·2²+10·2-3=65 ед. скорости.

__________________________________________________________________________________