ВЕРОЯТНОСТЬ СЛУЧАЙНОГО СОБЫТИЯ

Среди тех событий, которые могут произойти или не произойти при выполнении определенного комплекса условий на появление одного можно рассчитывать с большим основанием, на появление другого с меньшим, т.е. можно говорить о вероятности того или иного события.

Вероятность есть численная мера объективной возможности появления случайного события, она является его числовой характеристикой.

Существуют два метода определения вероятности случайного события: классический и статистический.

Классический метод определения вероятности основывается на равной возможности элементарных событий, образующих полную группу.

Допустим, бросается игральная кость, грани которой занумерованы цифрами 1, 2, 3, 4, 5, 6. Если кость совершенно однородна и имеет форму идеального правильного куба, то появление каждой из шести цифр при бросании кости - события равновозможные. Из равной возможности элементарных событий следует, что число их конечно и вероятности их могут быть определены априори. Событие А - появление цифры "3" на верхней грани игрального кубика при однократном бросании. Вероятность равна 1/6, т.е. она может быть определена как отношение числа случаев, благоприятствующих появлению этого события А к общему числу всех возможных случаев

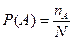, где n_A - число благоприятных случаев появления случайного события, N - общее число всех возможных испытаний.

В статистическом методе вводится понятие относительной частоты события. Пусть выполняется серия испытаний. В каждой серии определяется относительная частота появления интересующего нас события А. В любой серии испытаний через N обозначается общее число всех возможных появлений случайного события, а через n _i - число благоприятных исходов испытаний.

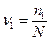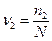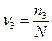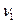
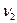
Тогда есть относительная частота появления события А в первой серии; во второй серии испытаний она равна , в третьей серии и т.д. Относительные частоты появления события А, полученные в разных сериях испытаний, т.е. 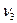и т.д. группируются около некоторого числа Р. Причем относительная частота события А тем ближе к указанному числу, чем больше количество испытаний в серии. Число Р,вокруг которого группируются относительные частоты события А в разных сериях испытаний, и есть вероятность события А.

Статистическая вероятность это предел, к которому стремится относительная частота события при бесконечном числе испытаний, т.е.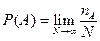

Исследователь Пирсон проводил серию испытаний с подбрасыванием монеты. После 12000 подбрасываний решка появлялась 0,5048 раз, после 24000 испытаний - 0,5012 раз, после 48000 испытаний частота появления решки равнялась - 0,5001, т.е. стремилась к ее классическому пределу 0.5.

Другой пример. Имеется несколько сосудов с газом - статистический ансамбль. Выделим в каждом сосуде элементарный объем. Пометим какую-то молекулу, и оценим сколько раз она появится в выделенном объеме в течении 10 минут.

Можно ли априори сказать сколько раз она появится в выделенном объеме в каждом из сосудов? - Нет.

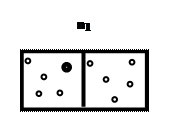
Более общий случай. Сосуд с газом: А - газ в одной половине сосуда, В - газ занимает весь объем. События несовместимые.

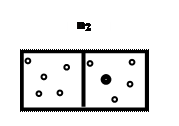
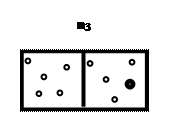
Относительная частота появления меченной молекулы в первом сосуде - 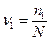, во втором - 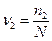, в третьем - .

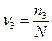Все частоты группируются около некоторого числа Р, т.е. статистической вероятностью будет предел, к которому стремятся относительные частоты отдельных испытаний.