Применение спектрального анализа при обработке геофизических данных.

Использование спектрального анализа в геофизике чрезвычайно широко и разнообразно. Основные приложения сводятся к следующему.

1.Оценка спектрального состава полезных сигналов (аномалий) и помех. Так, например, по спектральному составу волн в сейсморазведке максимум спектров полезных отраженных сигналов при среднечастотной сейсмике, используемой при поисках нефтегазовых залежей, приходится на диапазон от 20 до 60 Гц. В то же время, низкочастотные поверхностные (они же низкоскоростные) волны характеризуются диапазоном от 5 до 10Гц, а частотный состав микросейсм – от 0 до 450 Гц. Поэтому для выделения полезных сигналов требуется подавление как низкочастотных, так и высокочастотных составляющих общего спектра регистрируемых сигналов.

Аналогичная ситуация характерна для спектров аномалий потенциальных полей. Так, региональные аномалии являются низкочастотными, а спектр погрешностей аналогичен спектру микросейсм в сейсморазведке, т.е. для выделения локальных составляющих (аномалий) требуется также подавление как низкочастотных, так и высокочастотных составляющих.

2.Изучение спектров основных трансформаций, используемых в магнито-гравиразведке. На рис.5.1. приведены соответственно спектры операции осреднения поля в окне размером 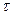(1), со спектром 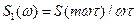; пересчета поля в верхнее полупространство на высоту Н (2) со спектром 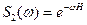; пересчета поля в нижнее полупространство на глубину Н (3) со спектром 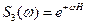; вычисления первой производной (4) и второй производной (5) со спектром 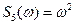; вычисления второй производной (5) на высоте Н, т.е. когда вначале производится пересчет поля на высоту Н, а затем для пересчитанного поля вычисляется вторая производная (6), со спектром 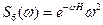. Если трансформации (1) и (2) подчеркивают низкочастотные составляющие, а трансформации (3) и (4) – высокочастотные составляющие, то трансформация (6) представляет полосовой фильтр.

3.Синтез сигналов по их спектрам. С этой целью используется построение спектров исходного поля, а затем с помощью обратного преобразования Фурье осуществляется вычисление значений сигнала в заданном из априорных соображений интервале частот.

4.Построение линейных, в частности, оптимальных фильтров и оценка погрешностей линейных фильтров, рассмотренных в разделах VI и VII.

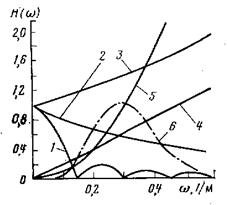
На рис.5.1. Спектры операции осреднения поля в окне (1), пересчета поля в верхнее полупространство (2); пересчета поля в нижнее полупространство (3); вычисления высших производных (4) и (5)

5.Комплексный анализ различных полей. Ввиду безразмерности спектров, спектры, полученные для разных полей, можно суммировать, перемножать и даже делить друг на друга. Получаемый при таких преобразованиях спектр комплексного анализа полей путем обратного преобразования приводит к комплексному параметру во временной или пространственной области.

Замечание 1. При обработке геофизических наблюдений по площади и по временному сейсмическому разрезу требуется использование двумерного дискретного преобразования Фурье. Разложение дискретного заданного сигнала в двумерный ряд Фурье имеет вид:

+

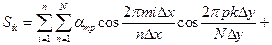
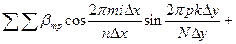
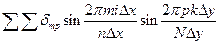
где m и p – номера гармоник по оси х и по оси y.

Коэффициенты Фурье при этом вычисляются по формулам

;

;

;

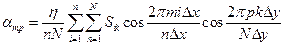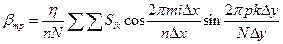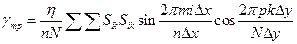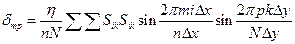
где 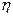=1, если m=0 и p=0; 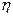=2, если m=0 или p=0; 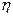=4, если m>0 и p>0.

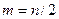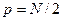Начало отсчета при вычислениях здесь помещено в начало координат системы X и Y, гармоники рассчитываются до значений и . По коэффициентам Фурье находится амплитудный спектр 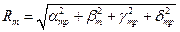, который изображается либо в виде изолиний, либо в виде графиков.

Замечание 2. При изучении геофизических полей на больших территориях (при длине профилей > 500 км) следует использовать разложение поля по сферическим функциям. Сферические функции являются комбинациями синусо-косинусных функций и функций Лежандра. При этом зависимость сферической функции от долготы определяется рядом Фурье, а от широты – функциями Лежандра

где - долгота, 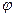- дополнение широты до 90⁰, а 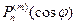- полином Лежандра первого рода степени n и порядка m.

Замечание 3. Рассматривая процесс вычисления амплитудного и фазового спектров, нетрудно видеть, что синусы и косинусы встречаются с одними и теми же аргументами. Алгоритм, позволяющий объединить их и тем самым ускорить процесс вычисления спектра, получил название алгоритма быстрого преобразования Фурье – БПФ.

Число арифметических операций в алгоритме БПФ, который уже требует числа исходных значений сигнала, равным 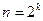, где k – целое число, равно 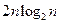, а при обычном преобразовании Фурье требуется n² операций, т.е. выигрыш равен отношению 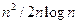. Так, при n=4096 и k=12 выигрыш вычислений по времени составляет 170 раз.