Свойства преобразований Фурье.
При спектральном анализе геофизических данных широко используются основные свойства преобразований Фурье, которые сводятся к следующему:
1) Свойство линейности, состоящее в том, что сумма сигналов 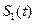 и
и 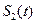 со спектрами
со спектрами 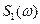 и
и 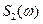 в спектральной области соответствует сумме их спектров: т.е.
в спектральной области соответствует сумме их спектров: т.е. 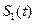 +
+ 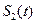
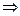
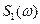 +
+ 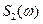 , а при умножении сигнала на число а, его спектр также умножается на это число, т.е.
, а при умножении сигнала на число а, его спектр также умножается на это число, т.е. 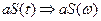 .
.
2) Свойство симметрии прямого и обратного преобразования Фурье для четных сигналов  .
.
3) Свойство подобия, заключающееся в том, что сжатие (растяжение) сигнала приводит соответственно к растяжению (сжатию) спектра, т.е. если 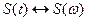 и а – константа, то
и а – константа, то  . Отсюда следует, что чем короче сигнал, тем спектр шире.
. Отсюда следует, что чем короче сигнал, тем спектр шире.
4) Свойство запаздывания сигнала на время 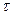 , приводящее к изменению фазового сдвига каждой гармоники на
, приводящее к изменению фазового сдвига каждой гармоники на 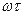 без изменения амплитудного спектра, т.е., если
без изменения амплитудного спектра, т.е., если 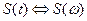 , то
, то 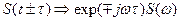 .
.
5) Свойство смещения спектра на величину 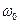 , приводящее к умножению сигнала на комплексное число, т.е.
, приводящее к умножению сигнала на комплексное число, т.е. 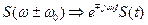
6) Свойство дифференцирования сигналов, состоящее в том, что если 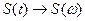 , то
, то 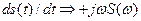 , т.е. дифференцирование сигнала приводит к обогащению спектра высокочастотными составляющими и уничтожает составляющие с нулевой частотой. Это свойство распространяется на производную любого порядка, т.е.
, т.е. дифференцирование сигнала приводит к обогащению спектра высокочастотными составляющими и уничтожает составляющие с нулевой частотой. Это свойство распространяется на производную любого порядка, т.е. 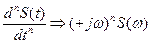 .
.
7) Свойство интегрирования сигнала 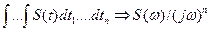 .
.
8) Свойство свертки двух сигналов. Сверткой двух сигналов 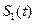 и
и 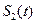 называется выражение
называется выражение 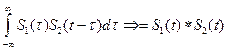 .
.
В частотной области свертка сигналов равна произведению спектров этих сигналов: 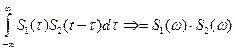 .
.
В частном случае свертки сигнала с сигналом обратного времени, т.е. когда 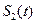 =
= 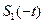 имеем
имеем 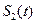
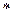
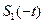
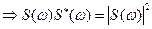 .
.
9) Свойство свертки двух спектров, состоящее в том, что свертка двух спектров равна произведению сигналов, т.е. 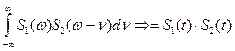 .
.
Дата добавления: 2016-01-16; просмотров: 1816;
