Глава II. Дискретность электронных и атомных состояний. 2 страница

Несколько позже Штерном были поставлены опыты по дифракции атомов и молекул на кристалле. Зависимость распределения максимумов интенсивностей была схожа с представленной на рис. 15 для электронов.

Все эти опыты привели к возникновению мысли о том, что все микрочастицы обладают волновыми свойствами. Причём, в волновых свойствах фотонов и других микрочастиц нет различия. В 1927 г. Луи де Бройль высказал предположение, что каждой движущейся частицы, мы можем поставить в соответствие некоторую длину волны. Подобную волну назвали в последствии волной де Бройля. Установим связь между параметрами волны и движущейся частицы.

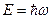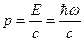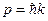
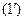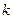1. Для волны де Бройля, как и для любой другой электромагнитной волны, мы можем записать: (1). С другой стороны, для импульса: ; , где - волновой вектор. Но для волнового вектора мы можем записать: 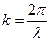, т. о. 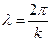; 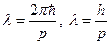. Из последней формулы следует выражение для волны де Бройля: 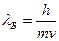(2). Из этого выражения следует интересный вывод, касающийся распределения интенсивностей в опытах с дифракцией электронов. Изменяя приложенную разгоняющую разность потенциалов, мы изменяем длину волны де Бройля. Когда выполняется условие Вульфа – Брэгга, возникает максимум.

2. Определим теперь фазовый вид волн де Бройля. Введём некоторые дополнительные определения. Фазовой скоростью называют скорость, 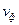с которой перемещается в пространстве фаза 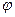плоской монохроматической волны 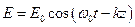, где 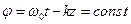(3). Другими словами, фазовая скорость – это скорость распространения точки постоянной фазы волны. Найдём эту скорость. Рассмотрим для этого выражение (3). Это уравнение чисто геометрически описывает плоскость, перпендикулярную к оси 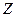, на которой постоянна фаза волны. Таким образом, эта плоскость является как бы траекторией движения точки постоянной фазы. Поэтому, чтобы найти её скорость, необходимо взять производную от (3) по времени. Получим: 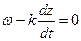, так как производная от константы будет ноль. Отсюда найдётся и фазовая скорость: 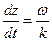. Это соотношение определяет как раз фазовую скорость. Найдём некоторые свойства фазовой скорости. 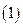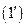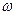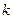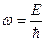Возвращаясь к уравнениям и , выразим из них и : и 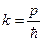. Основываясь на определении фазовой скорости и полученных выражениях, найдём другую форму записи для неё: 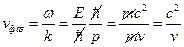. Здесь 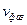– фазовая скорость волны, соответствующей частице; 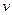– скорость самой частицы; 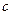– скорость света. Таким образом, как видно из полученной формулы, фазовая скорость будет больше скорости света, однако никакого противоречия с теорией относительности это не вызывает. Очевидно, что фазовая скорость не измерима в эксперименте. Измерить можно лишь так называемую групповую скорость.

3. Групповой скоростью называют величину, приближённо характеризующую распространение негармонической волны (которая является суперпозицией группы гармонических волн). Если форма волны изменяется в результате дисперсии1 волн в среде не очень быстро, то можно рассматривать распространение негармонической волны как целого с групповой скоростью, отличной от фазовых скоростей её гармонических составляющих. Групповая скорость характеризует скорость переноса энергии волной. По определению для групповой скорости мы можем записать: 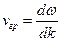(отсюда сразу становится понятным условие, ограничивающее скорость изменения 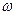). Возвращаясь к соотношениям, полученным для фазовой скорости, получим: 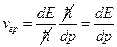. Таким образом, .

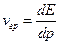4. Если волны распространяются в недиспрегирующей среде (фазовая скорость не зависит от частоты), то групповая скорость равна скорости движения частицы 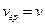. Тогда, вспоминая выражение для фазовой скорости 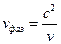, мы можем записать: 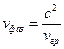. Из последней формулы следует: .

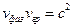Итак, мы установили, как связаны свойства частиц и волн де Бройля. Оценим теперь длину волны де Бройля. В опытах Девисона – Джермера ускоряющая разность потенциалов была 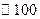В. Тогда для энергии электрона имеем выражение: 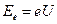. С другой стороны, кинетическая энергия электрона 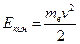. На основании закона сохранения энергии необходимо положить 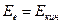или 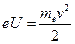. Так как импульс электрона будет 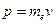, то 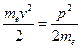, то есть 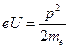. Отсюда 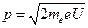. Так как 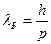, то 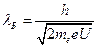. Оценивая численное значение 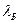, мы можем получить, что 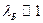Å.

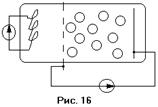
Рассмотрим теперь ещё один опыт. В 1921 г. немецкий физик Рамзауэр исследовал рассеяние электронов на атомах аргона при энергиях электрона от менее чем одного до нескольких десятков электрон-вольт. Обнаруженный им эффект назвали в последствии его именем. Он состоял в аномальной проницаемости некоторых газов (в частности аргона) для медленных электронов. Рассмотрим схему опыта (рис. 16).

Брался триод, в одной половине которого

электроны не ускорялись, а в другой ускорялись. Трубку триода наполняли инертным газом (аргон). Электрон, попадая с раскалённой нити катода в пространство триода,

движется по направлению к катоду и сталкивается с молекулой газа; при этом электрон рассеивается на ней. Поэтому, чем больше будет энергия электрона, тем больше шансов, что он пролетит без столкновения, то есть тем меньше вероятность рассеяния. Таким образом, с ростом ускоряющей разности потенциалов сила тока в цепи катод – анод должна возрастать. Графически зависимость между данными величинами можно представить так (см. рис. 17). 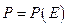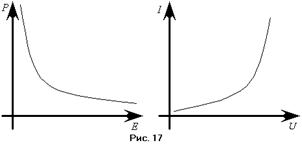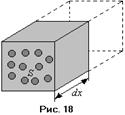Здесь зависимость есть зависимость вероятности рассеяния электрона от его энергии. Введём теперь в рассмотрение несколько новых величин, которые впоследствии помогут нам количественно описать эффект Рамзауэра. Будем рассматривать сечение рассеяния частиц. Понятие сечения рассеяния связано с вероятностью столкновения частицы с атомом или ядром. Будем считать частицу точечной. Пусть электрон падает на площадь 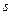объёма, в котором расположены молекулы с концентрацией 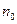(рис. 18). В слое толщиной 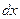в направлении движения электрона находится число молекул 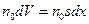, а сумма их поперечных сечений, которая как бы закрывает собой часть площади 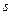, равна 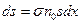, где 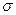- коэффициент пропорциональности. Отсюда следует, что вероятность попадания электрона в одну из молекул в слое 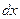будет равна: 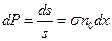. Как видно из полученной формулы, коэффициент 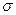имеет размерность площади: 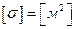, отсюда и название сечения рассеяния. Рассмотрим, как же можно найти сечение рассеяния. Пусть у нас есть поток частиц, движущихся в газообразной среде. Тогда, вследствие рассеяния, плотность потока частиц убывает на величину 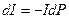. Если частица прошла путь 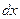, то 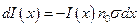. Решаем обыкновенное дифференциальное уравнение с разделяющимися переменными.

; . .

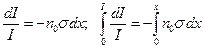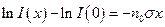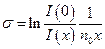Последняя формула позволяет из опыта получить значение коэффициента рассеяния.

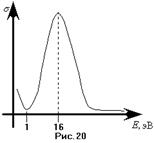
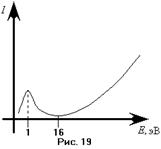
Введём теперь понятие длины свободного пробега. Так называют расстояние, пройденное частицей между двумя последовательными соударениями. Увеличение длины свободного пробега электрона напрямую связано с уменьшением вероятности столкновения его с молекулой; уменьшением сечения рассеяния. Следовательно, возрастает вероятность пролёта электрона между катодом и анодом без соударения с молекулой, то есть возрастает ток в цепи катод – анод. Длина свободного пробега пропорциональна энергии электрона. Таким образом, зависимость 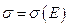будет иметь вид аналогичный указанному на первом из рисунков 17. Однако в действительности наблюдалась картина, указанная на рисунках 19 и 20. То есть при уменьшении энергии электрона от нескольких десятков электрон-вольт, сечение его рассеяния на аргоне растёт, как это и предсказывается теорией. Затем при энергии около 16 эВ поперечное сечение достигает максимума и при дальнейшем уменьшении энергии электрона уменьшается. При энергии электрона примерно 1 эВ сечение близко к нулю и затем начинает увеличиваться (см. рис. 20).

Увеличение сечения с ростом энергии электрона и тем более почти полное исчезновение рассеяния вблизи энергии 1 эВ нельзя понять с точки зрения классических представлений, так как при этой энергии атомы аргона становятся как бы не существующими для электронов, и электроны пролетают сквозь них без столкновения. Объясняется это так. Электрону мы можем поставить в соответствие волну де Бройля 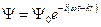. Тогда при некоторой длине волны де Бройля (она, как известно, зависит от энергии электрона), будет наблюдаться дифракционный максимум или минимум. Здесь молекула газа является препятствием, на котором рассеивается электронная волна. Условие, при котором происходит хорошо выраженная дифракция таково, что длина падающей волны должна быть порядка диаметра атома. Тогда, если рассматривать оптическую аналогию, за препятствием возникает светлое пятно, а не тень. То есть электрон проходит сквозь атом без отклонения и сечение его рассеяния на атоме близко к нулю.

Глава II. Дискретность электронных и атомных состояний.

§ 2.1.Законы излучения абсолютно чёрного тела.

К концу XIX века было завершено построение термодинамики и создана теория электромагнитных явлений. Термодинамика удовлетворительно описывала широкий круг явлений, связанных с веществом, то есть с корпускулярной формой материи. Теория электромагнетизма удовлетворительно описывала явления, связанные с электромагнитным полем и, в частности, с электромагнитными волнами и светом, электромагнитная природа которого была теоретически открыта Максвеллом. В форме электромагнитных волн электромагнитное поле обрело своё самостоятельное существование, независимое от зарядов и токов, которыми оно порождается. В науку вошло представление о полевой форме материи в виде излучения. Возник вопрос о законах взаимопревращения материи в полевой и корпускулярной форме, или, другими словами, вопрос о взаимопревращении излучения и вещества. Представлялось естественным, что этот вопрос можно решить в рамках классической физики, поскольку каждая из форм материи хорошо описывалась соответствующей классической теорией. Первое указание на недостаточность классической физики для понимания взаимоотношения этих форм материи было получено при изучении излучения чёрного тела. Из опыта известно, что раскалённые до высоких температур тела начинают светиться, то есть излучать электромагнитные волны видимого диапазона. При более низких температурах тела самостоятельно не светятся, но излучают преимущественно электромагнитные волны вне видимого диапазона. Поэтому, прежде всего, возник вопрос о законах этого излучения. Рассмотрим его. Для этого введём несколько вспомогательных понятий и определений.

Полной объёмной плотностью энергии излучения 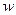называют энергию, приходящуюся на единицу объёма: 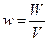. В случае электромагнитной волны мы можем записать: .

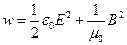Объёмной спектральной плотностью излучения называют объёмную плотность энергии излучения, приходящейся на единичный интервал частот: 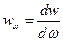. Полная объёмная плотность энергии излучения связана с объёмной спектральной плотностью излучения так: .

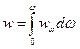Поглощающей способностью 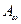называют отношение энергии 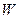поглощённой телом за одну секунду в интервале частот 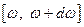ко всей энергии, излучённой за одну секунду в том же интервале частот: .

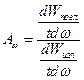Энергетической светимостью 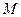называют энергию, излучённую участком поверхности тела за одну секунду: 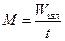. Отсюда для спектральной плотности светимости мы можем записать: 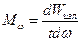(1).

Интенсивностью излучения называют энергию, проходящую за единицу времени через поверхность единичной площади 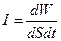. Соответственно, спектральной интенсивностью излучения называют энергию, проходящую за единицу времени через поверхность единичной площади в единичном интервале частот: 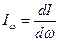. Очевидно, что интенсивность и спектральная интенсивность излучения связаны следующим соотношением: .

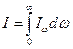Поток лучистой энергии, проходящей за время 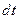через малую площадку 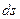в пределах телесного угла 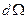, ось которого перпендикулярна площадке 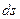, определяется следующим выражением: .

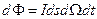Рассмотрим некоторый объём с телами, ограниченный адиабатической оболочкой. Через некоторое время между телами в полости установится термодинамическое равновесие. В этом состоянии температура всех тел постоянная. Тела излучают энергию. Такое излучение называется равновесным. Говорят, что такое излучение имеет равновесную спектральную плотность. Неравновесное же излучение образуется у живых организмов, атомов и т.д. Для равновесного излучения существует ряд законов.

Законы теплового излучения.

1. Закон Кирхгофа. Равновесная спектральная объёмная плотность излучения 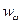зависит только от температуры и не зависит от свойств тел в адиабатической оболочке и свойств самой оболочки: .

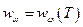2. 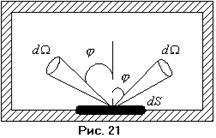Закон Кирхгофа. В состоянии термодинамического равновесия поглощённая за одну секунду участком поверхности тела энергия излучения, должна быть равна энергии излучённой за одну секунду тем же участком поверхности: 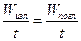. Установим связь между излучательной и поглощающей способностью тела. Так как эти величины характеризуют только поверхность самого тела и совершенно не зависят от окружающего излучения, то в рассуждениях относительно этого излучения можно вводить любые предположения. Предположим, что излучающее тело со всех сторон окружено равновесным излучением, температура которого равна температуре тела. Это, например, можно осуществить, если в качестве рассматриваемого участка поверхности тела взять часть внутренней поверхности замкнутой полости, температура стенок которой поддерживается постоянной. Выделим из всего излучения часть, составляющую интервал частот 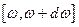, и рассмотрим превращения ей при излучении и отражении от стенок полости. На площадку 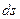стенки за время 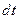в пределах телесного угла 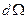падает поток лучистой энергии 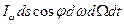. Часть его 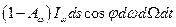отражается, остальная часть поглощается. Здесь добавляется множитель 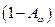, так как по определению 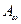есть поглощающая способность тел, а, соответственно, 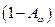– отражающая. На отражённый поток накладывается поток 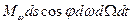собственного излучения площадки. Таким образом, от площадки 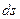внутрь полости исходит лучистый поток 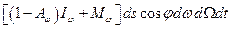. Но в состоянии равновесия тот же поток может быть представлен выражением 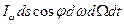. Приравнивая эти выражения, получим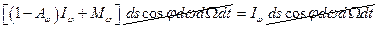 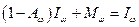; ; 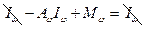; 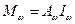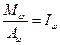. Покажем, что 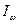зависит только от температуры. Вернёмся к определению 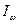: 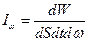. Распишем некоторые сомножители 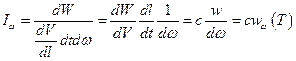. Таким образом, 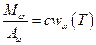, то есть чёрное тело не поглощает всё падающее на него излучение.

Вообще говоря, любое тело характеризуется степенью черноты. Так называю отношение поглощающей способности данного тела к поглощающей способности чёрного тела 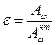. Тела, которые хорошо поглощают падающее на них излучение во всём интервале частот, называют серыми телами. Существуют абсолютно чёрные тела – тела, полностью поглощающие всё падающее на них излучение. Очевидно, что для них 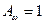, а второй закон Кирхгофа выглядит так: 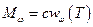. 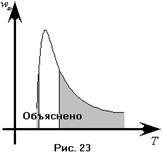Моделью абсолютно чёрного тела является полость с маленьким отверстием с посеребрёнными (зачернёнными) стенками. Классическая физика не смогла объяснить экспериментальную зависимость 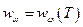. Вернее смогла, но только в рамках каких-то предельных случаев: пр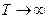и и 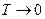(см. рис. 23). Исходя из соображений классической физики, попробуем получить выражение для объёмной спектральной плотности энергии излучения. Излучение в полости мы можем рассматривать как суперпозицию электромагнитных волн. Каждый тип волны будет характеризоваться своим пространственным распределением поле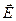й и 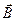. Каждый тип электромагнитных волн, обладающий определённым распределением поле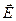й и 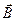, называется модой. Для удобства будем рассматривать в качестве полости куб с ребром 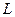. При определённых условиях в полости начнут распространяться стоячие волны, то есть волны, которые являются суперпозицией волн одинаковой частоты, распространяющихся в противоположных направлениях. В кубе (рис. 24) будет находиться группа стоячих волн. Условием образования стоячей волны в полости будет следующее: разность фаз волнами должна быть кратна 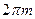: 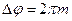. Не ограничивая общности, можно принять, что двукратное отражение от граней либо не вносит в фазу 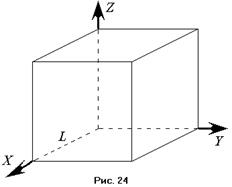волны никаких измерений, либо изменяет фазу на 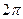. Поэтому условие образования стоячих волн в каждом из измерений куба 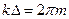, где 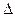– расстояние пройденное волной. Для нашего случая 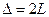или 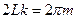. Для трёх групп стоячих волн имеем систему: 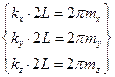, где 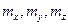– целые числа. Число волн 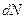, волновые числа которых заключены между 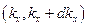, , 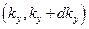, 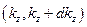равно числу целых чисел, заключённых в интервале 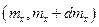, , 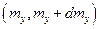, 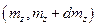и поэтому 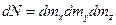или 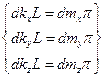. Тогда число волн, которые могут распространяться в полости с заданным интервалом частот, будет 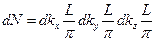; 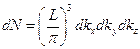(2). Пространство 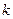есть пространство волновых векторов. Пусть у нас распространяются волны со всеми волновыми векторами. Тогда произведение 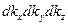даёт объём шарового слоя 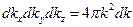. Так происходит потому, что каждая компонента произведения 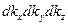есть проекция вектора 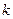на соответствующую ось, а если рассматривать вектор 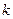в сферической системе координат, то произведению его компонент в декартовой системе координат будет соответствовать элементарный объём шарового слоя толщиной 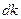. Тогда мы можем переписать (2) в виде: 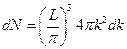. Учитывая, что независимых волн будет, на самом деле, в два раза меньше для каждой стороны куба, так как отражённую волну мы не учитываем, то тогда последнее выражение необходимо разделить на 8, так как 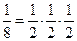. Тогда получим: 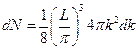. Перейдём теперь от 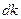к 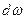: 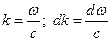. Последнее выражение в этом случае запишется в виде: 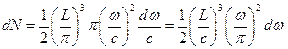. Тогда концентрация стоячих волн будет 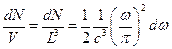. Поскольку электромагнитная волна обладает двумя возможными поляризациями, полная концентрация стоячих волн в два раза больше: 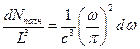. Мы получили формулу, определяющую концентрацию мод в полости. Вообще говоря, каждая из стоячих волн называется модой колебания, а число мод равно числу степеней свободы колебаний, которыми представлено излучение в полости. Теперь, если на каждую степень свободы будет приходиться средняя энергия 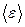, то плотность энергии излучения в полости будет равна 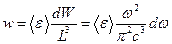. Таким образом, нахождение объёмной спектральной плотности энергии сводится к нахождению средней энергии, приходящейся на каждую стоячую волну в полости.