Статистические характеристики геополей.

Математической моделью при вычислении статистических атрибутов геофизических данных является случайная величина X, принимающая ряд дискретных значений X₁, X₂,…X_n. Такими значениями могут быть представлены измерения физических свойств горных пород и физических полей. Для оценки статистических характеристик последних, чаще всего, реализуется методика скользящего окна, что естественно и связано со статистической нестационарностью геополей. При измерениях поля по профилю, по трассе, по скважине окно - одномерное и содержит n-значений случайной величины, при площадных измерениях и при анализе временного разреза окно – двумерное, при обработке трехмерных данных окно трехмерное.

Для случайной величины X могут быть получены различные статистические характеристики. В настоящее время наиболее распространенным термином для статистических характеристик является атрибут. В качестве таких статистических атрибутов, рассчитываемых в скользящем окне, используются:

-среднее значение ;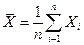

-дисперсия ;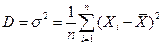

-среднеквадратическое отклонение ;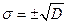

-асимметрия ;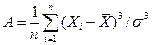

-эксцесс ;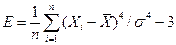

-медиана Ме или квантиль порядка 0,5, при котором вероятность Р значений случайной величины Х, больших или меньших Ме равны, т.е. ;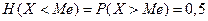

-коэффициент вариации .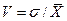

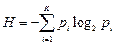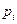-энтропия где - частость 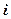-го интервала группирования, а K- число интервалов группирования.

Перечисленные выше статистические атрибуты широко используются при анализе как потенциальных, так и волновых полей. Среднее значение оказывается эффективным при выделении регионального тренда, дисперсия характеризует энергию поля, среднеквадратическое отклонение оценивает разброс вокруг среднего, асимметрия и эксцесс подчеркивают определенные детали поля, в частности, тектонические дислокации. В общем случае, при интерпретации полей статистических атрибутов, за исключением поля среднего значения, основной интерес представляют области их экстремальных значений. Их выделение позволяет более эффективно решать актуальную задачу районирования исследуемых территорий на стационарные области, по геофизическим данным, так как экстремальные значения статистических атрибутов, за исключением среднего значения, контролируют области нарушения статистической нестационарности геополей, которые в свою очередь приурочены к геологическим границам или тектоническим зонам.

Энтропия характеризует степень сложности (беспорядка) явления или объекта. Чем выше показатель энтропии, тем сложнее явление. Применительно к геофизике это означает, что если показатель энтропии стремится к нулю, то мы имеем дело с однородным полем. Это дает возможность проводить статистическое районирование по показателю энтропии (границы областей стационарности геополей будут характеризоваться зонами максимальных градиентов энтропии, в то время как сами объекты будут отмечаться относительно малыми значениями энтропии).