Оценка статистических и градиентных характеристик геофизических полей.
Одним из условий эффективного применения математических методов в определенной прикладной области является учет свойственных ей характерных особенностей. Использование математического аппарата без учета этого приводит к заведомо отрицательным результатам. В полной мере это касается применения методов вероятностно-статистического подхода, применяемых в процессе обработки и интерпретации геофизических данных.
Характерной чертой геолого-геофизических наблюдений является то, что они являются пространственно-временными, то есть любое измерение значения параметра, в общем случае, сопровождается набором атрибутов, определяющих его координаты в пространстве X,Y,Z и время наблюдения t. Другой важнейшей особенностью геофизических измерений является то, что выборки, получаемые в результате наблюдений случайного параметра в различных точках наблюдения, не являются однородными и представлены набором нескольких случайных величин. Это связано с естественным изменением статистических характеристик геополей в пространстве, то есть их статистической нестационарностью. Таким образом, изменяя состав выборки посредством отбора точек наблюдения в соответствии с их пространственным расположением, можно получать различные оценки статистических параметров, что в итоге приводит к неоднозначности конечных результатов.
При обработке геоданных часто приходится строить гистограммы. Гистограммаописывает распределение частот (или частостей) 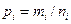 , определяемых для каждого значения
, определяемых для каждого значения 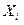 случайной величины Х. Для построения гистограммы весь диапазон значений Х разбивается на определенное число разрядов и подсчитывается число значений случайной величины
случайной величины Х. Для построения гистограммы весь диапазон значений Х разбивается на определенное число разрядов и подсчитывается число значений случайной величины 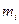 , приходящееся на каждый i-й разряд, которое затем нормируется на общее число значений случайной величины. По оси абсцисс для гистограммы откладываются разряды, соответствующие определенному диапазону значений случайной величины, а по оси ординат – соответствующие этим разрядам частоты (или частости)
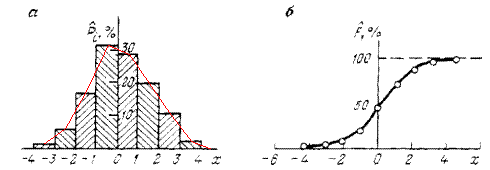
, приходящееся на каждый i-й разряд, которое затем нормируется на общее число значений случайной величины. По оси абсцисс для гистограммы откладываются разряды, соответствующие определенному диапазону значений случайной величины, а по оси ординат – соответствующие этим разрядам частоты (или частости) 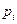 . В результате получают ступенчатую фигуру, состоящую из прямоугольников, которую и называют гистограммой рис.1,1.(а).
. В результате получают ступенчатую фигуру, состоящую из прямоугольников, которую и называют гистограммой рис.1,1.(а).
На основе гистограммы строится также статистическая функция распределения, называемая еще кумулятивной кривой. Если середины разрядов на гистограмме обозначить через х1, х2,…хr, то функция распределения F будет выражена как
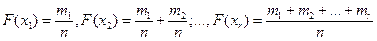
При построении гистограмм не существует строго обоснованных методов определения числа разрядов r. Обычно пользуются одним из трех эмпирических правил: 1) определяют 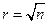 ; 2) r находятся по интервалу группирования данных ∆х, равного двойной или тройной погрешности измерения атрибута; 3) r определяют по величине ∆х, вычисляемой по формуле Стреджерса:
; 2) r находятся по интервалу группирования данных ∆х, равного двойной или тройной погрешности измерения атрибута; 3) r определяют по величине ∆х, вычисляемой по формуле Стреджерса:
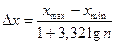 (1.1)
(1.1)
В каждом разряде гистограммы должно быть не менее пяти значений атрибута, в противном случае проводится объединение разрядов. Число разрядов также обычно не менее пяти.
Построение гистограмм и статистических функций распределений является основой обработки данных физических свойств горных пород и количественных атрибутов геофизических полей.
|
| Рис.1.1.Гистограмма (а) и кумулятивная кривая случайной величины (б). |
Кроме гистограмм, для графического представления того или иного распределения случайной величины, строят кумулятивную кривую (кривая накопленных частот). В прямоугольной системе координат строят точки с координатами 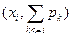 . Полученные точки соединяют отрезками рис.1.1(б). Если соединить ломаной линией центры вершин прямоугольников составляющих гистограмму, то получится кривая, получившая название полигон.
. Полученные точки соединяют отрезками рис.1.1(б). Если соединить ломаной линией центры вершин прямоугольников составляющих гистограмму, то получится кривая, получившая название полигон.
Дата добавления: 2016-01-16; просмотров: 935;
