Закон сохранения энергии. Запишем закон сохранения энергии в интегральной форме для объема
Запишем закон сохранения энергии в интегральной форме для объема 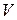
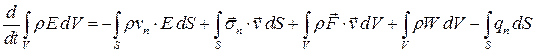 .
.
Перейдем к пределу при 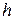 → 0 и примем формулы - , при этом
→ 0 и примем формулы - , при этом 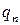 будем считать непрерывной функцией, т.е.
будем считать непрерывной функцией, т.е.
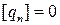 .
.
Получим
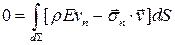 .
.
Отсюда, деля на 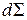 и устремляя
и устремляя 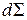 к нулю, получим
к нулю, получим
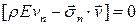
– закон сохранения полной энергии на скачке в точке  .
.
Итак, условия на поверхности сильного разрыва имеют вид
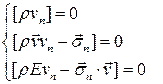
Здесь не выписано условие на момент количества движения, так как оно становится следствием баланса импульсов на скачке.
Проанализируем полученные условия, записав их применительно к совершенному газу, когда
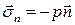 .
.
Имеем
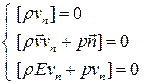
Здесь возможны два случая: поверхность разрыва распространяется по газу или покоится относительно него.
Пусть скачок и газ движутся с одной и той же скоростью, то есть
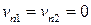 .
.
Такой разрыв называется контактным. Из баланса массы следует, что плотность с обеих сторон разрыва может принимать произвольные значения. Из баланса импульса, если его спроектировать на 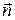 , следует, что давление непрерывно на разрыве. Уравнение баланса энергии выполняется тождественно. Касательная составляющая скорости
, следует, что давление непрерывно на разрыве. Уравнение баланса энергии выполняется тождественно. Касательная составляющая скорости 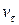 так же, как и плотность, может принимать произвольные значения с обеих сторон разрыва. Поэтому контактный разрыв также называют касательным или тангенциальным. Действительно,
так же, как и плотность, может принимать произвольные значения с обеих сторон разрыва. Поэтому контактный разрыв также называют касательным или тангенциальным. Действительно,
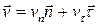 .
.
Из баланса импульса, если его спроектировать на 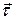 , следует, что
, следует, что
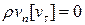 ,
,
то есть 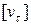 может быть не равным нулю.
может быть не равным нулю.
Итак, на контактном разрыве плотность и касательная составляющая скорости разрывны, а давление и нормальная скорость непрерывны.
Пусть поверхность сильного разрыва распространяется по газу, то есть
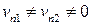 .
.
Такой разрыв называется ударной волной или скачком уплотнения. Запишем уравнение баланса импульсов в проекции на нормаль 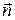
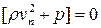
и на касательный вектор 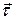
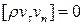
или
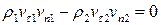 .
.
Так как, согласно балансу массы,
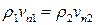 ,
,
то отсюда следует, что
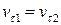 ,
,
то есть на ударной волне терпит разрыв только нормальная составляющая скорости газа, а касательная составляющая непрерывна.
Уравнение баланса энергии имеет вид
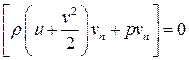 .
.
Перейдем к энтальпии. По определению
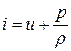 .
.
Тогда
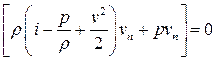
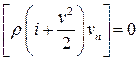 ,
,
или
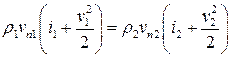 .
.
Так как
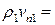
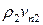 ,
,
то
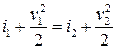 .
.
Кроме того
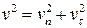 ,
,
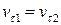 ,
,
поэтому баланс энергии принимает вид
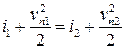 .
.
Окончательно, система балансовых уравнений на ударной волне имеет вид
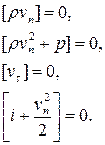
3.4.2. Соотношения на сильном разрыве
в неподвижной системе координат
Получим соотношения на сильном разрыве в неподвижной системе координат. Выкладки выполним на примере уравнения баланса импульса.
Интегральное уравнение баланса импульса для материального объема 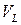 имеет вид
имеет вид
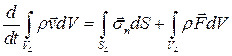 .
.
Пусть 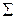 – поверхность разрыва. Рассмотрим два момента времени
– поверхность разрыва. Рассмотрим два момента времени 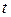 и
и 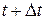 . Пусть в момент
. Пусть в момент 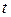
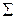 совпадает с материальной поверхностью
совпадает с материальной поверхностью 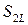 , а в момент
, а в момент 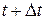 – с материальной поверхностью
– с материальной поверхностью 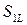 . Если
. Если 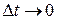 , то
, то 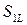 совпадает в пределе с
совпадает в пределе с 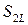 . Возьмем на
. Возьмем на 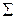 произвольную точку
произвольную точку  и получим соотношения на разрыве в этой точке. Рассмотрим малую плоскую окрестность
и получим соотношения на разрыве в этой точке. Рассмотрим малую плоскую окрестность 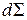 точки
точки  , перпендикулярную к нормали
, перпендикулярную к нормали 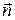 поверхности
поверхности 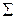 в точке
в точке  . Нормаль направим в сторону перемещения поверхности
. Нормаль направим в сторону перемещения поверхности 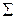 . Продолжим нормаль в обе стороны от точки
. Продолжим нормаль в обе стороны от точки  до пересечения с поверхностями
до пересечения с поверхностями 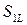 ,
, 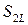 и построим прямой цилиндр с образующими, нормальными к
и построим прямой цилиндр с образующими, нормальными к 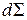 и проходящими через границу
и проходящими через границу 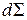 . Осью цилиндра является отрезок нормали в точке
. Осью цилиндра является отрезок нормали в точке  между поверхностями
между поверхностями 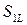 ,
, 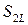 . Основания обозначим
. Основания обозначим 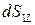 ,
, 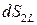 .
.
Применим к построенному материальному цилиндру 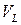 уравнение баланса импульса
уравнение баланса импульса
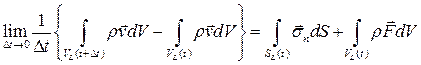
Вычислим объемы 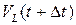 и
и 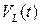 . Обозначим параметры сплошной среды перед разрывом индексом 1, за разрывом – 2, скорость поверхности разрыва в точке
. Обозначим параметры сплошной среды перед разрывом индексом 1, за разрывом – 2, скорость поверхности разрыва в точке  через
через 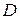 . Площадь основания цилиндра равна
. Площадь основания цилиндра равна 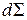 , а высота зависит от времени. В момент
, а высота зависит от времени. В момент 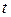 разрыв находится на
разрыв находится на 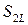 , через отрезок времени
, через отрезок времени 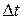 он переместится на
он переместится на 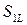 со скоростью
со скоростью 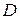 . Поверхность
. Поверхность 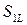 в течение
в течение 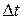 движется со скоростью
движется со скоростью 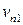 , а поверхность
, а поверхность 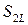 имеет скорость
имеет скорость 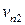 .
.
В момент 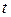 поверхность
поверхность 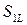 должна находиться на таком расстоянии от
должна находиться на таком расстоянии от 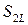 (разрыва), чтобы через
(разрыва), чтобы через 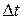 разрыв догнал
разрыв догнал 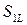 , т.е. высота цилиндра в момент
, т.е. высота цилиндра в момент 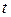 должна быть
должна быть 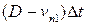 (Рис. 3.4.2).
(Рис. 3.4.2).
За время 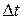 разрыв проходит расстояние
разрыв проходит расстояние 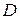
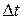 , а поверхность
, а поверхность 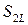 расстояние
расстояние 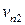
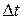 , поэтому высота цилиндра в момент
, поэтому высота цилиндра в момент 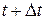 равна
равна 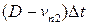 (Рис. 3.4.2).
(Рис. 3.4.2).
Распишем интеграл по 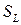 как сумму трех интегралов по основаниям и боковой поверхности цилиндра. Применим теорему о среднем к интегралам в уравнении . Получим
как сумму трех интегралов по основаниям и боковой поверхности цилиндра. Применим теорему о среднем к интегралам в уравнении . Получим
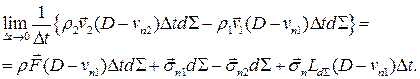
Знак минус перед 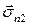 обусловлен тем, что нормали к
обусловлен тем, что нормали к 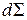 и
и 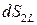 разнонаправлены.
разнонаправлены.
Перейдем к пределу при 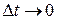 , потом поделим на
, потом поделим на 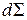 и перейдем к пределу при
и перейдем к пределу при 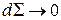 (стягиваем окрестность к точке
(стягиваем окрестность к точке  ). В результате получим баланс импульса на разрыве в точке
). В результате получим баланс импульса на разрыве в точке  в неподвижной системе координат
в неподвижной системе координат
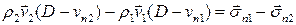
или
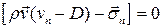 .
.
Аналогично можно получить балансовые соотношения для массы и энергии в неподвижной системе координат.
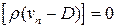 ,
,
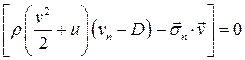 .
.
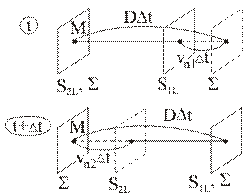 Рис. 3.4.2
Рис. 3.4.2
|
3.4.3. Соотношения на разрыве в системе координат,
связанной с покоящимся газом
Пусть перед ударной волной газ покоится, а волна бежит по нему со скоростью 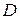 . Получим условия на ударной волне в неподвижной системе координат, связанной с покоящимся газом. Обозначим через
. Получим условия на ударной волне в неподвижной системе координат, связанной с покоящимся газом. Обозначим через 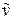 – нормальную к поверхности скачка скорость газа за скачком, тогда скорости в подвижной и неподвижной системе координат связаны соотношением
– нормальную к поверхности скачка скорость газа за скачком, тогда скорости в подвижной и неподвижной системе координат связаны соотношением
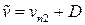
или
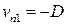 ,
, 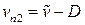 .
.
Подставим в , получим
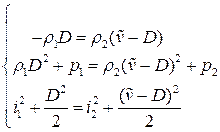 .
.
В силу баланса массы
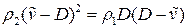 .
.
Поэтому баланс импульса примет вид
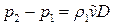 .
.
Таким образом, условия на ударной волне в неподвижной системе координат, когда газ перед волной покоится, имеют вид
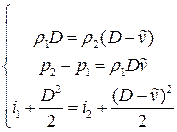 .
.
Дата добавления: 2015-12-29; просмотров: 1652;
