Подобие и моделирование явлений

Теория подобия изучает условия подобия физических явлений и является основой моделирования явлений. Физическое моделирование основано на замене исследования интересующего нас явления исследованием аналогичного явления на лабораторной модели с тем, чтобы по результатам лабораторных экспериментов сделать выводы о свойствах, характере, закономерностях исходного явления.

Физическое подобие является обобщением понятия геометрического подобия. При физическом подобии поля соответствующих физических параметров двух систем подобны в пространстве и времени. В частности, механическое подобие предполагает наличие геометрического, кинематического и динамического подобий. При кинематическом подобии должно быть подобие полей скоростей для двух рассматриваемых движений, при динамическом – соответствующих силовых полей.

Каждый процесс имеет ряд определяющих параметров. Из этих параметров могут быть составлены безразмерные комбинации, называемые критериями подобия. Условием подобия исходного и модельного процессов является равенство численных значений критериев подобия. Значения размерных физических параметров подобных процессов или систем могут сильно отличаться друг от друга, но значения безразмерных критериев подобия должны совпадать.

В качестве примера рассмотрим задачу моделирования движения жидкости в трубах. Пусть труба гладкая, круглая с диаметром 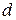и имеет бесконечную длину, чтобы не учитывать особенности входного и выходного участков течения. Течение будем считать установившимся, жидкость несжимаемой, имеющей плотность 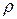и вязкость 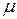. Средняя скорость жидкости равна 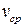. Зная среднюю скорость, можно определить перепад давления вдоль трубы и расход жидкости в единицу времени через поперечное сечение трубы.

Следовательно, труба, жидкость и состояние движения жидкости в целом определяются системой четырех определяющих параметров

.

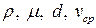Все механические характеристики движения являются функциями этих параметров. Из них можно образовать только одну независимую безразмерную комбинацию

,

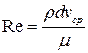которая называется числом Рейнольдса. Все другие комбинации являются функциями числа Рейнольдса. Например, коэффициент сопротивления трубы для течения Пуазейля равен

.

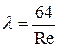В других случаях, когда нельзя получить выражение для коэффициента сопротивления через число Рейнольдса теоретически, задача сводится к отысканию функциональной зависимости 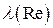. Эту функцию можно найти экспериментальным путем, проводя опыты по движению, например, воды в одной какой-нибудь трубе и измеряя сопротивление в зависимости от скорости воды. Полученные результаты можно использовать при рассмотрении движения других жидкостей и в трубах с другими диаметрами. Критерием подобия при этом является число Рейнольдса, а условием подобия – условие равенства значения числа Рейнольдса для исходного и модельного течений.