Анализ взаимосвязи явлений, возникающих в организации
Между явлениями общественной жизни существует взаимосвязь. Она проявляется между признаками явлений, а, следовательно, и между характеризующими их показателями.
Статистической анализ информации с целью установления взаимосвязи общественных явлений позволяет во многих случаях выразить ее в виде количественных соотношений. Зная, например, степень влияния определенных факторов на показатели эффективности производства, можно в реальности создать условия для получения наилучшего результата.
Функциональные и корреляционные связи. Взаимосвязи между показателями подразделяются на функциональные и корреляционные. При функциональной связи размер результативного показателя полностью обусловливается размерами одного или нескольких факторных показателей. Например, площадь круга прямо пропорциональна квадрату радиуса окружности, ограничивающей ее. Производительность труда (выработка) прямо пропорционально зависит от уровня норм выработки и нормативов обслуживания (производительной силы труда), степени интенсивности труда, продолжительности рабочего дня и рабочего периода. Однако надо иметь ввиду, что в то же время существует зависимость уровня норм выработки и нормативов обслуживания (производительной силы труда) от изменения интенсивности труда, продолжительности рабочего дня и продолжительности рабочего периода, т.е. изменение одних факторов причинно обусловливается изменением других. Функциональная связь между факторным показателем 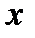 и результативным
и результативным 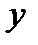 обычно выражается формулой:
обычно выражается формулой:
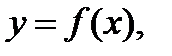
где 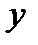 – функция;
– функция; 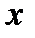 – аргумент.
– аргумент.
Но такой подход к характеристике взаимосвязи межу результативным показателем и показателями, выступающими в качестве факторов не раскрывает взаимосвязь, существующую между факторами и играющую существенную роль в формировании динамики результативного показателя. Абстрагирование от нее необходимо на определённом этапе исследования, но не должно исключать ее раскрытия и изучения.
При корреляционной связи нет строгого соответствия между размерами результативного и факторных показателей. В этом случае одному и тому же размеру факторного показателя, как правило, соответствует несколько размеров результативного показателя. Например, рабочие, имеющие одинаковый тарифный разряд (одинаковую квалификацию), могут производить за смену различное количество деталей. Поэтому при корреляционной связи между признаками при изменении факторного показателя изменяется лишь средний размер результативного показателя.
Определенное представление о взаимосвязи двух показателей можно получить, если первичные данные о них представить графически в виде корреляционного поля, т. е. совокупности точек, координаты которых соответствуют размерам факторного и результативного показателей (рис. 23.1). Из рис. 23.1 следует, что между расстоянием перевозки и сроком доставки грузов существует прямая зависимость, поскольку большинство точек на графике располагается в определенном порядке по направлению из левого нижнего угла в правый верхний угол корреляционного поля. Тот факт, что точки не образуют прямую линию, свидетельствует о корреляционной связи между показателями, а их скученность – о тесноте связи, т. е. о высокой степени зависимости результативного показателя от факторного.
Взаимосвязь между показателями может быть однофакторной и многофакторной. При однофакторной связи один показатель выступает как причина, а другой – как следствие. При многофакторной связи причиной выступает значительное число показателей, а результатом (следствием)–один. Для ее выявления и количественной характеристики применяют различные методы, в частности аналитические группировки, корреляционный и факторный анализ.
Метод аналитических группировок.Взаимосвязь между результативным и одним из факторных показателей в определенных случаях может быть выявлена при помощи аналитических группировок. Для этого целесообразно использовать корреляционную таблицу (табл. 23.6). Она, как рациональная форма группировки единиц совокупности по двум показателям, позволяет сделать заключение о характере связи между показателями на основе расположения частот. Если наибольшие размеры частот располагаются примерно по диагоналям таблицы (сверху вниз или снизу-вверх), то в первом случае имеется прямая связь между показателями, а во втором – обратная.
Таблица 23.6
Зависимость продолжительности доставки повагонных отправок от расстояния перевозки (данные условные)
| Рассто-яние пере-возки, тыс. км | Всего отправок | В том числе со сроком доставки, сут. | Общее время доставки, отправко-сут. | Средняя продолжительность достави,сут. |
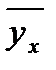
| ||||||||
| до 4 | 4– | 8– | 12–16 | 16–20 | 20–24 | 24–28 | 18 и более | ||||||
| А | |||||||||||||
| До 0,5 | – – | – | – | – | – | 4,00 | 1,81 | ||||||
| 0,5–1,0 | – | – | – | – | 4,37 | 4,18 | |||||||
| 1,0–1,5 | – | – | – | 5,54 | 6,55 | ||||||||
| 1,5–2,0 | – | – | – | – | 6,00 | 8,93 | |||||||
| 2,0–2,5 | – | – | – | 9,33 | 11,30 | ||||||||
| 2,5–3,0 | – | – | – | – | 15,43 | 13,67 | |||||||
| 3,0–3,5 | – | – | – | – | – | – | 15,20 | 16,04 | |||||
| 3,5–4,0 | – | – | – | – | 16,46 | 18,41 | |||||||
| 4,0 и более | – | – | 23,58 | 20,78 | |||||||||
| Итого | 8,768 | 8,768 |
Примечание. Общее время доставки в отправко-сут (графа 10), получено по данным середины интервалов (графа А) и соответствующим их частотам (графы 2-9): по первой строке 2٠42+6٠15+10٠9=264; по второй строке 2٠45+6٠21+10٠6+14٠4=332 и т.д.
Средние групповые размеры результативного показателя по данным табл. 23.5 определяются суммированием произведений размеров этого показателя на соответствующие частоты каждой группы, выделенной по факторному показателю и делением полученных показателей на численность единиц групп (см. графу 11 табл. 23.6), т. е. по формуле средней арифметической взвешенной. Соединив на графике точки, изображающие групповые средние, получим ломаную линию, которую называют линией эмпирическойрегрессии. Из сопоставления граф А и 11 табл. 23.6 видно, что с увеличением расстояния перевозки продолжительность доставки груза растет.
По материалам аналитической группировки можно оценить тесноту связи с помощью эмпирического корреляционного отношения
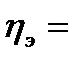 √
√ 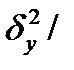
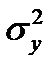 , ( 23.7)
, ( 23.7)
где 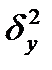 – межгрупповая дисперсия результативного показателя;
– межгрупповая дисперсия результативного показателя;
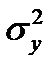 – общая дисперсия результативного показателя.
– общая дисперсия результативного показателя.
В зависимости от тесноты связи между показателями корреляционное отношение может принимать размеры от нуля до единицы. Это вытекает из правила сложения дисперсии (см. гл.6). При функциональной зависимости в каждую группу, выделенную по конкретному размеру факторного показателя, попадут единицы с одинаковыми размерами результативного показателя, а поэтому групповые дисперсии будут равны нулю. Следовательно, в этом случае 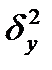 =
= 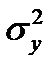 , а
, а 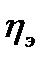 = 1,0.
= 1,0.
Если связь между показателями отсутствует, то в группы, выделенные по размеру факторного показателя, попадут единицы совокупности, распределяющиеся по размеру результативного показателя примерно одинаково, а поэтому групповые средние размеры показателя ( 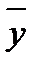 ) не будут существенно отличаться друг от друга. Следовательно, в этом случае
) не будут существенно отличаться друг от друга. Следовательно, в этом случае 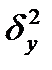 будет стремиться к нулю, и корреляционное отношение
будет стремиться к нулю, и корреляционное отношение 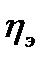 будет иметь размер близкий к нулю.
будет иметь размер близкий к нулю.
Таким образом, при отсутствии зависимости между показателями эмпирическое корреляционное отношение 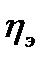 = 0, а при функциональной – равно 1. Следовательно, чем ближе корреляционное отношение к единице, тем теснее связь между рассматриваемыми показателями.
= 0, а при функциональной – равно 1. Следовательно, чем ближе корреляционное отношение к единице, тем теснее связь между рассматриваемыми показателями.
Для оценки тесноты связи между расстоянием перевозки и сроками доставки, выполним расчет 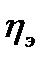 по данным табл. 23.6.
по данным табл. 23.6.
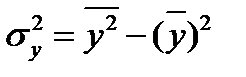 =139,092 - 76,878=62,214;
=139,092 - 76,878=62,214;
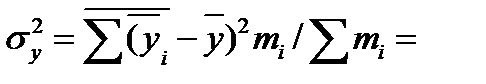
= [(1,81-8,768)266+(4,18-8,768)2 76+(6,55-8,768)2 70+...+(20,78-8,768)2 43]/(66+76+70+...+43) =43,440.
Подставив размеры показателей 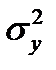 и
и 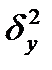 в формулу (23.6), получим:
в формулу (23.6), получим:
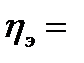 √43,440/62,214 =0,836.
√43,440/62,214 =0,836.
Полученный результат свидетельствует о том, что связь между расстоянием перевозки и сроком доставки грузов достаточно тесная.
Регрессионно-корреляционный анализ взаимосвязи. Показатели и методы корреляции и регрессии используются в статистике для решения двух задач:
выражения корреляционной зависимости в виде аналитического уравнения (математической модели);
оценки тесноты связи между результативным и факторными показателями.
Решение сформулированных задач регрессионно-корреляционного анализа иллюстрируем на однофакторной и многофакторной моделях.
Парная прямолинейная зависимость (однофакторная модель). Зависимость между результативным и одним факторным показателями может быть выражена уравнением определенного вида. Покажем это на примере зависимости продолжительности доставки грузов от расстояния перевозки (см. табл. 23.6).
Время (продолжительность) доставки груза 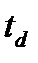 складывается из времени нахождения его на станции отправления и назначения
складывается из времени нахождения его на станции отправления и назначения 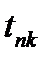 и времени следования от станции отправления до станции назначения , т.е.
и времени следования от станции отправления до станции назначения , т.е. 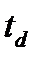 =
= 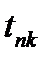 +
+ 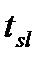 .
.
Время следования груза можно выразить формулой 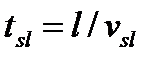 ,
,
где 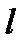 – расстояние перевозки груза, км;
– расстояние перевозки груза, км;
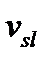 – скорость перемещения груза от станции отправления до станции назначения, км/сут.
– скорость перемещения груза от станции отправления до станции назначения, км/сут.
В результате продолжительность доставки груза можно представить следующим образом:
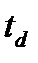 =
= 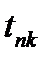 +
+ 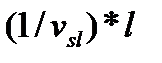 . (23.8)
. (23.8)
Формула позволяет сделать вывод, что, между продолжительностью доставки груза и расстоянием его перевозки существует прямая зависимость.
В уравнении (23.8) 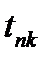 и
и 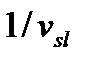 являются варьирующими показателями, поэтому при исследовании зависимости между
являются варьирующими показателями, поэтому при исследовании зависимости между 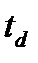 и
и 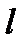 следует абстрагироваться от их изменения. Для это следует вместо конкретных размеров показателей использовать их типичные размеры, т.е. средние. Обозначив
следует абстрагироваться от их изменения. Для это следует вместо конкретных размеров показателей использовать их типичные размеры, т.е. средние. Обозначив 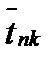 через
через 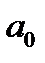 , а
, а 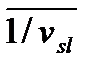 через
через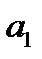 , получим:
, получим:
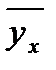 =
= 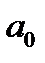 +
+ 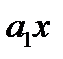 , (23.9)
, (23.9)
где 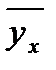 – результативный показатель, зависящий от факторного показателя
– результативный показатель, зависящий от факторного показателя 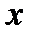 .
.
Уравнение (23.9)называется уравнением прямолинейной связи или прямолинейной регрессии, а постоянные показатели 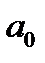 и
и 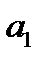 – параметрами уравнения.
– параметрами уравнения.
По заданным размерам 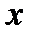 и
и 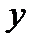 параметры уравнения определяются по способу наименьших квадратов. Применение этого способа к уравнению (23.8) дает следующую систему нормальных уравнений:
параметры уравнения определяются по способу наименьших квадратов. Применение этого способа к уравнению (23.8) дает следующую систему нормальных уравнений:
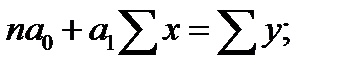
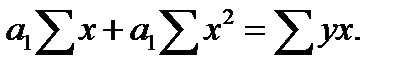 . (23.10)
. (23.10)
Поскольку в расчетах используются материалы корреляционной таблицы (см табл. 23.6), то система уравнений (23.10) в принятых обозначениях будет иметь следующий вид:
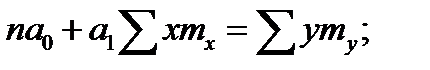
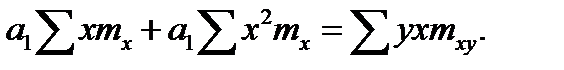 ( 23.11)
( 23.11)
где 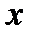 – средины интервалов, образованных по факторному показателю;
– средины интервалов, образованных по факторному показателю;
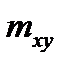 – частоты в клетках таблицы, показывающие, сколько единиц совокупности обладает одновременно определенными размерами показателя
– частоты в клетках таблицы, показывающие, сколько единиц совокупности обладает одновременно определенными размерами показателя 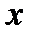 и
и 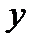 .
.
Выполнив по данным табл. 23.6, расчеты найдем:
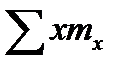 =0,25∙66+0,75∙76+1,25∙70+1,75∙47+2,25∙18+2,75∙14+
=0,25∙66+0,75∙76+1,25∙70+1,75∙47+2,25∙18+2,75∙14+
+3,25∙10+3,75∙26+4,25∙43 =635,0;
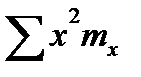 =0,252∙66+0,752∙76+1,252∙70 +1,752∙47+2,252∙18 +2,752∙14+
=0,252∙66+0,752∙76+1,252∙70 +1,752∙47+2,252∙18 +2,752∙14+
+3,252∙10+3,752∙26+4,252∙43 =1745,15;
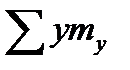 =2∙134+6∙99+10∙29+14∙49+18∙17+22∙16+26∙8+ 30∙18 =3244;
=2∙134+6∙99+10∙29+14∙49+18∙17+22∙16+26∙8+ 30∙18 =3244;
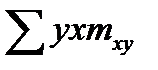 = 0,25∙264+0,75∙332+1,25∙388+1,75∙282+2,25∙168+2,75∙216+ +3,25∙152+3,75∙428+4,25∙1014=8674,0.
= 0,25∙264+0,75∙332+1,25∙388+1,75∙282+2,25∙168+2,75∙216+ +3,25∙152+3,75∙428+4,25∙1014=8674,0.
Подставив эти размеры показателей в систему нормальных уравнений (23.11), получим:
370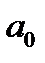 +635
+635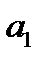 = 3244 ;
= 3244 ;
635 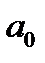 +1745,16
+1745,16 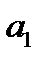 =8674.
=8674.
Решив эту систему уравнений, найдем: 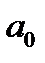 = 0,632,
= 0,632, 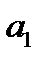 =4,740. Следовательно, зависимость продолжительности доставки грузов от расстояния перевозок выражается уравнением
=4,740. Следовательно, зависимость продолжительности доставки грузов от расстояния перевозок выражается уравнением
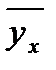 = 0,632+4,740
= 0,632+4,740 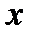 .
.
Это уравнение может быть использовано для расчета средней продолжительности доставки грузов при различной дальности перевозки (см. графу 12 табл. 23.6).
Для оценки тесноты связи между признаками у и х следует использовать коэффициент корреляции
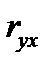 = (
= ( 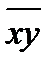 -
- 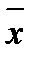
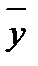 )/
)/ 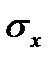
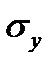 ,
,
где 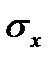 и
и 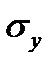 – средние размеры квадратических отклонений
– средние размеры квадратических отклонений 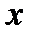 и
и 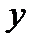 ;
;
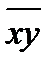 – средний размер произведения
– средний размер произведения 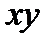 :
:
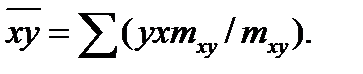
Размер коэффициента корреляции 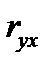 находятся в пределах от -1 до +1. При отсутствии связи между показателями
находятся в пределах от -1 до +1. При отсутствии связи между показателями 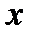 и
и 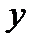
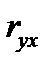 = 0, при функциональной зависимости между ними
= 0, при функциональной зависимости между ними 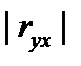 =1.
=1.
Коэффициент корреляции 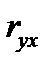 будет иметь положительный знак при прямой зависимости
будет иметь положительный знак при прямой зависимости 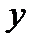 от
от 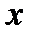 (
( 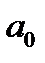 > 0) и отрицательный – при обратной (
> 0) и отрицательный – при обратной ( 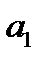 < 0) .
< 0) .
Выполнив расчет линейного коэффициента корреляции на основе данных табл. 23.6 получим:
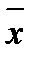 = 635 /370 = 1,716;
= 635 /370 = 1,716; 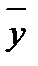 = 8,768;
= 8,768; 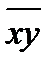 =8674/370= 23,443;
=8674/370= 23,443;
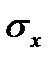 = √ 1745,16/370- (1,716)2 = 1,331;
= √ 1745,16/370- (1,716)2 = 1,331; 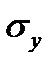 = √62,314 =7,888;
= √62,314 =7,888;
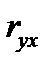 = (23,443 - 1,716 ٠8,768) /(1,331٠7,888) = 0,800.
= (23,443 - 1,716 ٠8,768) /(1,331٠7,888) = 0,800.
Коэффициент корреляции, равный 0,800 свидетельствует о наличии достаточно тесной связи между расстоянием перевозки и продолжительностью доставки грузов.
Для оценки тесноты связи между 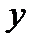 и
и 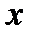 может быть использован индекс корреляции
может быть использован индекс корреляции 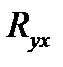 , рассчитываемый по формуле
, рассчитываемый по формуле
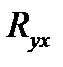 = √(
= √( 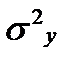 -
- 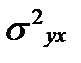 )
) 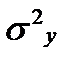 ,
,
где 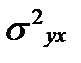 =
= 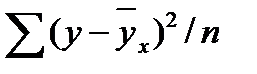 , т. е. средний квадрат отклонений заданных размеров
, т. е. средний квадрат отклонений заданных размеров 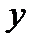 от полученных по формуле
от полученных по формуле 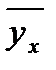 =
= 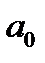 +
+ 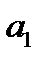
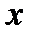 .
.
При функциональной зависимости 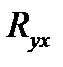 = 1, поскольку в этом случае
= 1, поскольку в этом случае 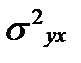 = 0. При отсутствии связи между
= 0. При отсутствии связи между 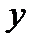 и
и 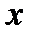
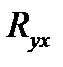 = 0, ибо в этом случае фактически
= 0, ибо в этом случае фактически 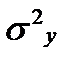 =
= 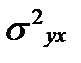 .
.
Для определения тесноты связи между показателями 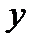 и
и 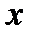 на основе исходных данных о результативном признаке
на основе исходных данных о результативном признаке 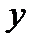 и данных полученных по уравнению
и данных полученных по уравнению 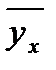 =
= 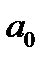 +
+ 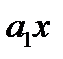 ,может быть рассчитано теоретическое корреляционное отношение
,может быть рассчитано теоретическое корреляционное отношение
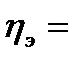 √
√ 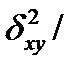
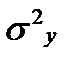 ,
,
где 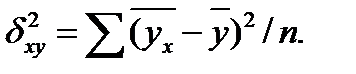
Для уравнения 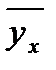 =
= 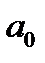 +
+ 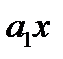 коэффициент корреляции, индекс корреляции и теоретическое корреляционное отношение равны между собой.
коэффициент корреляции, индекс корреляции и теоретическое корреляционное отношение равны между собой.
Многофакторная модель (множественная корреляция). Примером множественной корреляции может служить зависимость себестоимости 10 единиц приведенной продукции от динамической нагрузки груженого вагона, от соотношения порожнего и груженого пробега и от участковой скорости движения поезда. Уравнение этой связи имеет следующий вид
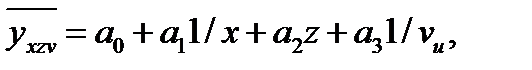 (23.12)
(23.12)
где 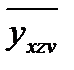 – себестоимость 10 единиц приведенной продукции , руб./10 т-км;
– себестоимость 10 единиц приведенной продукции , руб./10 т-км;
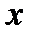 – динамическая нагрузка груженого вагона, т/ваг.;
– динамическая нагрузка груженого вагона, т/ваг.;
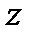 – соотношение порожнего и груженого пробега вагонов, %;
– соотношение порожнего и груженого пробега вагонов, %;
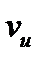 – участковая скорость движения поезда, км/ч.
– участковая скорость движения поезда, км/ч.
Для определения параметров уравнения связи используется система нормальных уравнений составленных по способу наименьших квадратов:
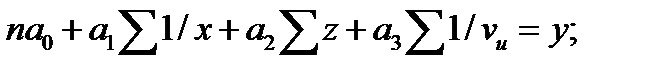
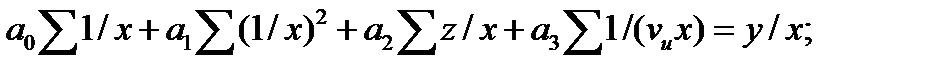 (23.13)
(23.13)
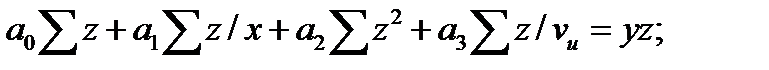
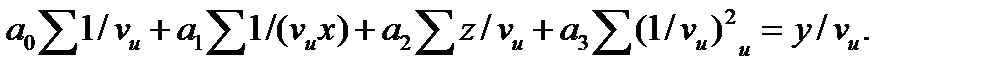
Для оценки тесноты связи 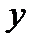 c
c 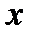 ,
, 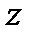 ,
, 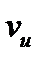 определяется индекс множественной корреляции Ryxzv :
определяется индекс множественной корреляции Ryxzv :
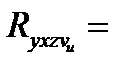 √(
√( 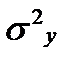 -
- 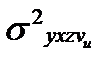 ) /
) / 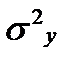 ,(23.14)
,(23.14)
где 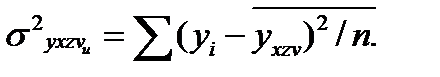
Для примера используем данные о размере приведенной продукции отделений железной дороги, расчет размера которой производился для этого вида подразделений в период плановой экономики, которые имели статус юридических лиц, и определяющих ее факторах.
На основе исходных данных составим табл. 23.7, а также рассчитаем параметры системы уравнений (23.13) и индекс множественной корреляции (23.14).
Таблица 23.7
Себестоимость 10 единиц приведенной продукции отделений железной дороги и определяющие ее факторы (по материалам 40 отделений ), (данные условные)
| Себестоимость 10 т-км, руб. | Динамическая нагрузка груженого вагона, т | Соотношение порожнего и груженого пробега,% | Участковая скорость движения поездов, км/ч. | Себестоимость 10-т-км, руб. | Динамическая нагрузка груженого вагона, т | Соотношение порожнего и груженого пробега,% | Участковая скорость движения поездов, км/ч. | Себестоимость 10-т-км, руб. | Динамическая нагрузка груженого вагона, т | Соотношение порожнего и груженого пробега,% | Участковая скорость движения поездов, км/ч. | ||||||||||
| 145,2 | 54,57 | 40,6 | 32,7 | 84,9 | 54,99 | 45,1 | 40,5 | 76,9 | 57,74 | 38,8 | 42,4 | ||||||||||
| 151,9 | 53,38 | 47,8 | 38,8 | 124,1 | 56,93 | 42,6 | 35,8 | 96,8 | 54,07 | 32,4 | 45,7 | ||||||||||
| 153,8 | 54,84 | 40,1 | 40,3 | 151,4 | 43,55 | 38,8 | 27,8 | 99,2 | 53,48 | 41,1 | 47,2 | ||||||||||
| 54,1 | 50,63 | 32,5 | 39,7 | 143,2 | 54,84 | 41,7 | 33,4 | 84,9 | 55,38 | 46,5 | 40,8 | ||||||||||
| 91,8 | 58,81 | 33,7 | 38,2 | 153,7 | 54,37 | 49,1 | 38,2 | 124,2 | 57,26 | 44,8 | 35,5 | ||||||||||
| 160,7 | 54,65 | 41,5 | 30,5 | 153,2 | 54,82 | 42,4 | 40,6 | 151,1 | 46,14 | 41,3 | 27,6 | ||||||||||
| 96,6 | 58,63 | 35,5 | 35,9 | 84,2 | 51,31 | 41,2 | 39,3 | 115,3 | 54,53 | 40,6 | 32,6 | ||||||||||
| 120,1 | 54,14 | 38,6 | 34,1 | 93,9 | 57,66 | 40,1 | 39,1 | 151,9 | 54,39 | 49,3 | 38,8 | ||||||||||
| 87,9 | 56,16 | 39,1 | 38,6 | 160,4 | 56,31 | 44,2 | 30,6 | 155,6 | 54,82 | 42,1 | 40,5 | ||||||||||
| 99,2 | 54,45 | 37,6 | 35,8 | 94,5 | 59,76 | 35,9 | 35,5 | 84,3 | 51,31 | 41,5 | 39,0 | ||||||||||
| 83,6 | 59,28 | 38,5 | 44,1 | 120,8 | 54,46 | 36,0 | 34,4 | 92,5 | 57,63 | 40,1 | 39,6 | ||||||||||
| 75,9 | 57,27 | 39,2 | 43,4 | 89,7 | 57,44 | 38,1 | 38,6 | 149,6 | 56,27 | 44,3 | 30,7 | ||||||||||
| 94,5 | 53,46 | 32,3 | 45,7 | 99,6 | 52,86 | 38,6 | 36,4 | ||||||||||||||
| 97,3 | 52,92 | 39,4 | 47,3 | 82,6 | 59,82 | 36,2 | 42,8 | ||||||||||||||
На первом этапе получим систему уравнений с четырьмя неизвестными:
40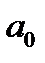 +0,7316
+0,7316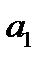 +1612,2
+1612,2 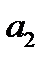 + 1,0691
+ 1,0691 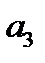 = 4531,1;
= 4531,1;
0,7316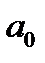 + 0,0134
+ 0,0134 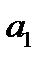 + 29,4893
+ 29,4893 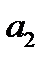 + 0,0197
+ 0,0197 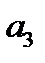 = 83,2591;
= 83,2591;
1612,2 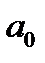 + 29,4893
+ 29,4893 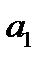 + 65638,0
+ 65638,0 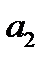 + 43,3290
+ 43,3290 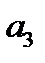 = 185706,4;
= 185706,4;
1,0691 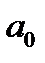 + 0,0197
+ 0,0197 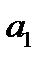 + 43,3290
+ 43,3290 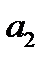 + 0,0298
+ 0,0298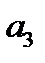 = 123,6272.
= 123,6272.
Решив ee получим: 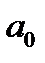 = -141,3825;
= -141,3825; 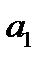 =4746,3489;
=4746,3489; 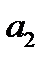 = 3,6096 и
= 3,6096 и 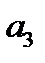 = 836,6773. Подставив эти размеры параметров в уравнение 23.13, получим, что:
= 836,6773. Подставив эти размеры параметров в уравнение 23.13, получим, что:
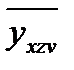 =-141,3825 +4746,3489(1/х) +3,6096z+836,6773(1/ vu). (23.14)
=-141,3825 +4746,3489(1/х) +3,6096z+836,6773(1/ vu). (23.14)
Учитывая, что 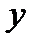 = 4531,1;
= 4531,1; 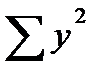 =549748,73, а
=549748,73, а 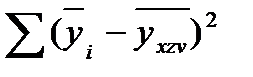 = 21381,64 , найдем:
= 21381,64 , найдем:
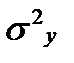 = 549748,73/40 -(4531,1/40)2 = 911,926;
= 549748,73/40 -(4531,1/40)2 = 911,926;
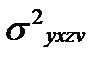 = 21381,64/40 = 534,5409.
= 21381,64/40 = 534,5409.
Следовательно, 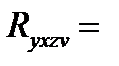 √ (911,926 - 534,5409)/911,926 = 0,643.
√ (911,926 - 534,5409)/911,926 = 0,643.
Данный размер индекса множественной корреляции свидетельствует о тесной связи себестоимости 10 единиц приведенной продукции отделения с выбранными факторами. Поэтому уравнение (23.14), полученное на основе данных достаточно большой совокупности, может быть использовано для практических целей.
Индекс множественной корреляции также может быть рассчитан по данным о размерах парных коэффициентов корреляции. Индекс множественной корреляции может быть рассчитан по данным о размерах парных коэффициентов корреляции. 4 ttKM+srhzso0STLpdE/8odMDPnTYfJ0uTsHx8+Vx/TrVzluza6sP46rkOVXq/m4+7kFEnOMfDL/6 rA4lO9X+QiYIqyDdZGtGFSzSDAQD2Wa7AlHzYgeyLOT/AuUPAAAA//8DAFBLAQItABQABgAIAAAA IQC2gziS/gAAAOEBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsBAi0A FAAGAAgAAAAhADj9If/WAAAAlAEAAAsAAAAAAAAAAAAAAAAALwEAAF9yZWxzLy5yZWxzUEsBAi0A FAAGAAgAAAAhAIo/VPEeAgAANwQAAA4AAAAAAAAAAAAAAAAALgIAAGRycy9lMm9Eb2MueG1sUEsB Ai0AFAAGAAgAAAAhAAV8PAXeAAAACAEAAA8AAAAAAAAAAAAAAAAAeAQAAGRycy9kb3ducmV2Lnht bFBLBQYAAAAABAAEAPMAAACDBQAAAAA= "/>
Для этих целей рекомендуется использовать формулу:
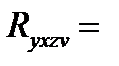 √ (
√ ( 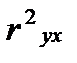 +
+ 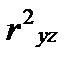 -
- 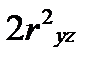
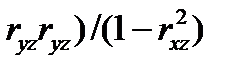 ,
,
где 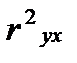 ,
, 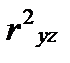 ,
, 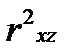 – коэффициенты парной корреляции соответ ственно между
– коэффициенты парной корреляции соответ ственно между 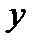 и
и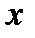 ,
, 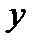 и
и 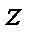 ,
, 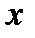 и
и 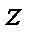 .
.
Условия применения корреляционного анализа в статистике. При использовании корреляции для анализа взаимосвязи общественных явлений на основе статистической информации необходимо соблюдать следующие условия:
построению корреляционных моделей (уравнений регрессий) должен предшествовать качественный анализ, т. е. выяснение наличия и особенностей взаимосвязей изучаемых явлений, исходя из их экономической сущности;
при построении многофакторных корреляционных моделей следует включать в них ограниченное число (примерно не более 8–10-ти) наиболее существенных и не дублирующих друг друга факторов;
при определении показателей корреляции следует пользоваться достаточно большим массивом первичной информации.
Необходимость соблюдения этих условий обусловлена особенностями корреляционного анализа.
Предварительный качественный анализ необходим для решения вопроса о включении конкретных факторов в модель множественной регрессии. Формальный подход к этому, т. е. включение в модель факторов без выяснения характера их влияния на результативный показатель, может привести к получению результатов, противоречащих фактам и логике. Таковым, например, может быть вывод, что рост соотношения порожнего и груженого пробега вагонов приводит к снижению себестоимости перевозки грузов. Такой же нелогичный результат может быть получен, если в модель будут включены дублирующие друг друга факторы.
Включение в модель множественной регрессии значительного числа факторов обычно повышает ее качество, поскольку в этом случае усложняется, а в ряде случаев становится невозможным установление характера связи между рассматриваемыми показателями, по существу. Использование различного рода количественных критериев, которые применяют при решении вопроса о включении данного фактора в модель, приводит к тому, что полученные параметры уравнений теряют реальный смысл. (При включении или исключении факторов обычно изменяются не только размеры параметров уравнений, но и знаки при них, т. е. вместо плюса появляется минус, а вместо минуса – плюс, что свидетельствует о ненадежности получаемых моделей).
К искажению результатов корреляционного анализа может также привести использование сводной информации, а также недостаточность ее объема, т.е. малая численность исследуемой совокупности.
Использование сводной информации вместо первичной, например, размеров средних групповых показателей вместо размеров конкретных показателей, приводит к искажению показателей тесноты связи. Это обусловлено тем, что при определении показателей тесноты связи применяются различные виды дисперсий, размеры которых изменяются в зависимости от степени обобщения информации, используемой при их расчете. Если, например, при определении общей дисперсии 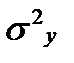 , входящей в формулы (23.7) и (23.14), вместо размеров вариантов будут использованы средние размеры групповых , то
, входящей в формулы (23.7) и (23.14), вместо размеров вариантов будут использованы средние размеры групповых , то 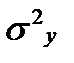 уменьшится на размер межгрупповой дисперсии, что неизбежно приведет к завышению размеров показателей тесноты связи. Тем не менее, необходимо учитывать, что информация о некоторых явлениях дает обобщенную характеристику.
уменьшится на размер межгрупповой дисперсии, что неизбежно приведет к завышению размеров показателей тесноты связи. Тем не менее, необходимо учитывать, что информация о некоторых явлениях дает обобщенную характеристику.
Для получения надежных показателей корреляции необходимо пользоваться значительными объемами информации. Это обусловлено тем, что при недостаточном объеме изучаемой совокупности могут быть получены существенные размеры показателей тесноты связи даже в том случае, когда между признаками связь отсутствует. Так, расчеты показывают, что размер коэффициента корреляции, рассчитанного по данным 10 единиц, случайно отобранных из генеральной совокупности, в которой связь между признаками отсутствует, может находиться в пределах до 0,71.
Для определения надежности показателей корреляции применяются формулы математической статистики. В частности, для определения надежности коэффициента корреляции может быть использована формула среднего размера квадратической ошибки
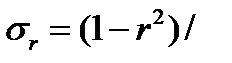 √ n-1 ,
√ n-1 ,
где 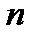 – количество наблюдений.
– количество наблюдений.
Если 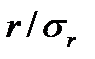 > 3 (при
> 3 (при 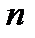 > 50), то коэффициент корреляции считается надежным.
> 50), то коэффициент корреляции считается надежным.
Факторный анализ взаимосвязи. Он включает показатели и методы исследования взаимосвязи общественных явлений: аналитические группировки, корреляционный анализ, метод главных компонент, дисперсионный анализ и др. Названные методы применяются в тех случаях, когда связь между показателями носит корреляционный характер. Однако многие показатели статистики связаны между собой функционально. Так, размер оборотного капитала организации, авансированного на наем рабочей силы в среднем за период 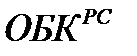 равен произведению издержек производства на наем рабочей силы
равен произведению издержек производства на наем рабочей силы 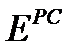 на продолжительность оборота этой части оборотного капитала
на продолжительность оборота этой части оборотного капитала 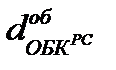 деленную на календарную продолжительность периода для которого производится расчет оборотного капитала(
деленную на календарную продолжительность периода для которого производится расчет оборотного капитала( 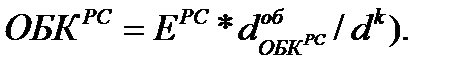
Для исследования таких взаимосвязей показателей в статистике применяются специальные способы, которые являются составной частью факторного анализа. Для количественной характеристики относительного влияния факторов на результативные показатели, между которыми имеется функциональная зависимость, обычно используются индивидуальные и общие индексы (см. п. 8.1).
Роль отдельных факторов в образовании абсолютного прироста результативного признака в значительной мере зависит от формы взаимосвязи между результативным и факторными показателями и степени изменения факторов.
В тех случаях, когда уровень результативного показателя определяется как алгебраическая сумма нескольких факторных, то его абсолютный прирост равен алгебраической сумме абсолютных приростов каждого из факторных признаков, т. е.
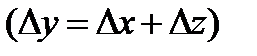 .
.
Так, продолжительность оборота оборотного капитала, авансированного на наем рабочей силы равна сумме элементов оборота этой части капитала
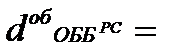
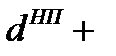
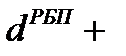
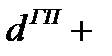
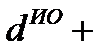
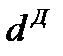 ,.
,.
где 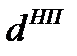 – время нахождения форме незавершенного производства, дни;
– время нахождения форме незавершенного производства, дни;
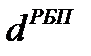 – время нахождения в форме расходов будущих периодов, дни;
– время нахождения в форме расходов будущих периодов, дни;
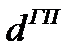 – время нахождения в форме готовой продукции, дни;
– время нахождения в форме готовой продукции, дни;
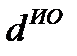 – время нахождения в форме изделий отгруженных, сданных работ и оказанных услуг, дни;
– время нахождения в форме изделий отгруженных, сданных работ и оказанных услуг, дни;
. 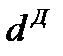 - время нахождения в форме денег, дни.
- время нахождения в форме денег, дни.
Следовательно, изменение продолжительности оборота оборотного капитала, авансированного на наем рабочей силы складывается под влиянием изменения каждого элемента оборота. Абсолютный прирост (снижение) каждого элемента оборота будет характеризовать размер изменения за его счет результативного показателя (продолжительности оборота оборотного капитала, авансированного на наем рабочей силы.
Относительное влияние изменения каждого элемента оборота на динамику продолжительности оборота капитала можно характеризовать путем расчета темпа прироста продолжительности оборота капитала делением абсолютного прироста определенного элемента оборота 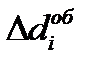 на продолжительность оборота оборотного капитала за базисный период
на продолжительность оборота оборотного капитала за базисный период 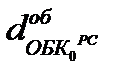 . т.е. по формуле
. т.е. по формуле
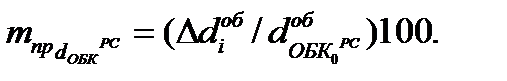 .
.
Если результативный показатель является произведением нескольких факторных показателей, то в этом случае абсолютный прирост результативного показателя можно выразить следующим образом
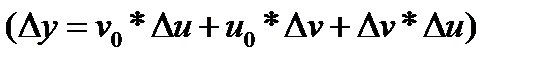 , (23.15)
, (23.15)
где 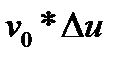 – изолированное влияние фактора
– изолированное влияние фактора 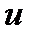 ;
;
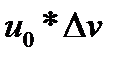 – изолированное влияние фактора
– изолированное влияние фактора 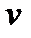 ;
;
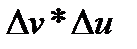 –результат совместного влияния обоих факторов.
–результат совместного влияния обоих факторов.
Размер совместного влияния обоих факторов 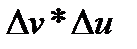 (рис. 23.2) не может быть однозначно распределен между ними на основе научно обоснованных принципов.
(рис. 23.2) не может быть однозначно распределен между ними на основе научно обоснованных принципов.
В связи с этим задача разложения абсолютного прироста результативного показателя за счет факторов имеет несколько вариантов решения. Из формулы (23.15) видно, что если прирост одного из факторов равен нулю, то абсолютный прирост результативного показателя полностью обусловливается изменением другого фактора. Вполне определенный вывод о размере влияния факторов можно сделать в том случае, если абсолютный прирост результативного показателя и одного фактора имеют одинаковый знак (плюс или минус), а прирост второго фактора – противоположный знак. В этом случае вполне обоснованно можно утверждать, что абсолютный прирост результативного показателя произошел за счет того фактора, прирост которого имеет тот же знак, что и абсолютный прирост результативного показателя. Например, при абсолютном приросте оборотного капитала, авансированного на наем рабочей силы, и снижении продолжительности оборота этой части оборотного капитала, можно сделать вывод, что прирост оборотного капитала произошел за счет увеличения издержек на наем рабочей силы.
При изменении результативного показателя и обоих факторных в одном и том же направлении, совместное влияние факторов может быть распределено между ними пропорционально размеру изменения результативного показателя за счет изолированного влияния каждого из них.Затем полученные результаты распределения добавляются к показателям изолированного влияния. .
Однако возможен и другой вариант решения вопроса, основанный на принятых принципах построения индексов количественных (объемных) и качественных показателей. Для примера рассмотрим индексы денежного выражения стоимости реализованной продукции, физического объема продукции и цен. В этом случае для оценки размера влияния факторов возникает задача распределения абсолютного прироста денежного выражения стоимости реализованной продукции 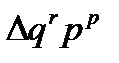 между факторами: физическим объемом реализованной продукции
между факторами: физическим объемом реализованной продукции 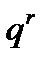 и ценами продажи
и ценами продажи 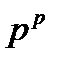 . При принятой системе построения индексов факторов произведение индекса физического объема реализованной продукции и индекса цен продажи равно индексу денежного выражения стоимости реализованной продукции (
. При принятой системе построения индексов факторов произведение индекса физического объема реализованной продукции и индекса цен продажи равно индексу денежного выражения стоимости реализованной продукции ( 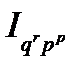 =
= 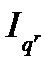
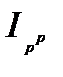 ) , что можно также представить следующим образом :
) , что можно также представить следующим образом :
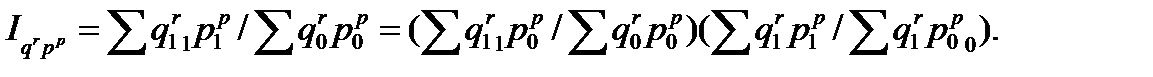
Из формулы взаимосвязи показателей следует, что абсолютный прирост денежного выражения стоимости реализованной продукции складывается из абсолютных приростов обусловленных изменением физического объема реализованной продукции 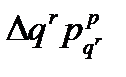 и изменения цен продажи
и изменения цен продажи 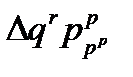 ,что можно представить так:
,что можно представить так:
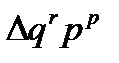 =
= 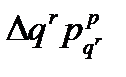 +
+ 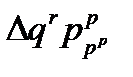 .
.
Расчет абсолютного прироста денежного выражения стоимости продукции за счет каждого фактора производится на основе агрегатных формул индексов как разница между их числителями и знаменателям.
Если 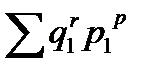 = 15,0 млн руб.;
= 15,0 млн руб.; 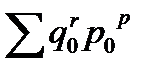 = 10,9 млн руб., а
= 10,9 млн руб., а 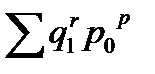 = 14,1 млн руб.
= 14,1 млн руб.
Тогда 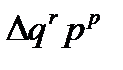 = 15,0-10,9=4,1 млн руб.;
= 15,0-10,9=4,1 млн руб.;
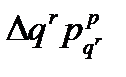 = 14,1-10,9 = 3,2 млн руб.;
= 14,1-10,9 = 3,2 млн руб.;
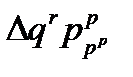 = 15,0 - 14,1= 0,9 млн руб.
= 15,0 - 14,1= 0,9 млн руб.
На основе абсолютного прироста денежного выражения стоимости реализованной продукции в целом и изолированного влияния каждого фактора можно определить удельный вес его влияния. В нашем примере удельный вес влияния каждого фактора на изменение денежного выражения стоимости реализованной продукции соответственно составил:
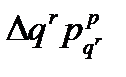 /
/ 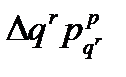 = 3,2/4,1= 0,780 или 78,0 %, и
= 3,2/4,1= 0,780 или 78,0 %, и 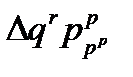 /
/ 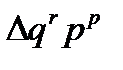 = 0,9/4,1 = 0,220 или 22,0%. Отсюда следует, что абсолютный прирост денежного выражения стоимости реализованной продукции на 78,0% обусловлен ростом количества реализованной продукции и на 22% – ростом цен продажи.
= 0,9/4,1 = 0,220 или 22,0%. Отсюда следует, что абсолютный прирост денежного выражения стоимости реализованной продукции на 78,0% обусловлен ростом количества реализованной продукции и на 22% – ростом цен продажи.
В рассмотренном варианте разложения совместного влияния факторов 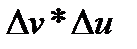 между факторами использована система взвешивания факторных индексов.
между факторами использована система взвешивания факторных индексов.
В процессе анализа статистической информации встречаются зависимости, имеющие вид у = vuz или у =v / и. В таких случаях размер абсолютного прироста результативного показателя за счет каждого фактора может определяться на основе изложенных принципов.
Дата добавления: 2016-01-18; просмотров: 1282;
