Трехлетние скользящие показатели и средние размеры
Погрузки грузов на филиале, млн т
| Год | По-гру- жено за год | Подвижная трехгодичная сумма (погружено за 3 года) | Ско-льзя- щий средний размер | Год | По-гру- жено за год | Подвижная трехгодичная сумма (погружено за 3 года) | Ско- льзя- щий сред- ний размер |
| 88,6 | - | - | 73,9 | 225,7 | 75,2 | ||
| 88,2 | 266,4 | 88,8 | 74,6 | 221,6 | 73,9 | ||
| 89,6 | 253,4 | 84,5 | 73,1 | 223,3 | 74,4 | ||
| 75,6 | 242,4 | 80,8 | 75,6 | 222,5 | 74,2 | ||
| 77,2 | 226,7 | 75,6 | 73,8 | _ | _ |
Скользящие средние размеры показателя характеризуют практически плавное снижение погрузки грузов.
Скользящие средние размеры показателя обычно привязываются к серединам соответствующих интервалов. Если укрупненный интервал охватывает нечетное число уровней ряда, то его середина всегда совпадает с конкретным периодом или датой. Так, в приведенном примере первый скользящий средний размер относится к 2006 г. (середина приходится на второй уровень укрупненного интервала).
Если укрупненный интервал охватывает четное число уровней ряда, то его середина не совпадает с конкретным периодом или датой. Так, при шестиуровневом интервале середина первого интервала будет находиться между третьим и четвертым уровнями, середина второго между четвертым и пятыми уровнями и т.д.
Для того, чтобы можно было отнести подвижные средние размеры показателя к конкретному периоду или дате, прибегают к их центрированию. Оно заключается в том, что на основе подвижных средних размеров показателя рассчитываются в свою очередь двухуровневые скользящие средние размеры показателя. Допустим, что определены следующие четырехуровневые подвижные средние размеры показателя:
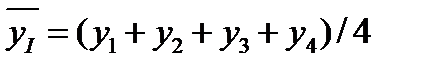 ;;
;;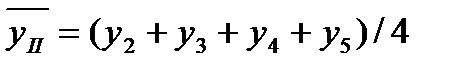
.
Тогда двухуровневый средний скользящий размер показателя из скользящих средних (  +
+ 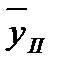 ) /2 будет приходиться на период (дату), к которому относится
) /2 будет приходиться на период (дату), к которому относится 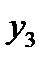 ; следующий двухуровневый скользящий средний размер показателя , (
; следующий двухуровневый скользящий средний размер показателя , ( 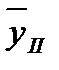 +
+  )/2 – за период (дату), к которому относится
)/2 – за период (дату), к которому относится 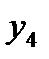 и т.д.
и т.д.
Позволяя установить тенденцию развития явления, методы укрупнения интервалов и скользящих средних размеров показателя не дают возможности выразить основную тенденцию развития явления в виде аналитической формулы. Вместе с тем такое выражение тренда имеет большое познавательное и практическое значение, поскольку не только дает представление об основном направлении изменения показателя, но и позволяет рассчитать уровень явления для тех периодов, для которых эти сведения отсутствуют, а самое главное на перспективу.
При аналитическом сглаживании рядов динамики, прежде всего, выясняют, какое аналитическое уравнение наиболее адекватно отображает изменение конкретного явления. Если, например, абсолютная скорость изменения уровня явления примерно постоянна, то вполне логично использовать уравнение прямой, а если относительная скорость непостоянна (наблюдается ускорение) – то параболы второго порядка.
Рассмотрим приемы аналитического сглаживания данных на примере динамики погрузки цветных металлов в филиале ОАО «РЖД» - железной дороге. Как видно из графы 1 табл. 23.10, погрузка цветных металлов увеличивается, хотя в отдельные годы наблюдается и спад.
В этих условиях вполне допустимо предположение, что изменение погрузки цветных металлов происходит непрерывно и с постоянной скоростью. Поэтому для аналитического сглаживания исходных данных вполне логично применить уравнение прямой.
Таблица 23.10
Динамика погрузки цветных металлов на филиале ОАО « РЖД - железной дороге (данные условные)
| Год | Погрузка цветных металлов yi , тыс. т | t | t2 | yi t | Сглаженные размеры погрузки грузов 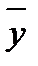 t , тыс. т t , тыс. т
|
| А | |||||
| 99,9 | -3 | -299,7 | 98,9 | ||
| 95,4 | -2 | -190,8 | 97,3 | ||
| 94,8 | -1 | -94,8 | 95,7 | ||
| 96,7 | – | – | – | 94,1 | |
| 93,5 | 93,5 | 92,6 | |||
| 88,4 | 176,8 | 91,0 | |||
| 90,3 | 270,9 | 89,4 | |||
| Итого | 659,0 | – | -44,1 | 659,0 |
Обозначив погрузку цветных металлов через уi , а время – через t, получим уравнение прямой:


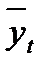 =
= 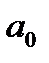 +
+ 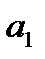
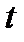 , (23.16)
, (23.16)
где 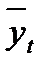 – сглаженные размеры
– сглаженные размеры  .
.
Параметры этого уравнения 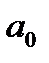 и
и 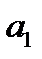 определяются по исходным данным на оcнове системы нормальных уравнений по способу наименьших квадратов:
определяются по исходным данным на оcнове системы нормальных уравнений по способу наименьших квадратов:
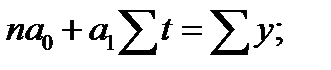
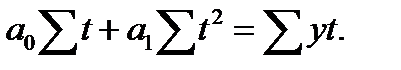
где 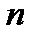 – число уровней ряда динамики (в нашем примере
– число уровней ряда динамики (в нашем примере 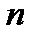 = 7).
= 7).
Система нормальных уравнений примет более простой вид, если время 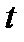 обозначить так, чтобы
обозначить так, чтобы 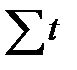 = 0. При нечетном числе уровней ряда динамики
= 0. При нечетном числе уровней ряда динамики 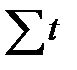 = 0, если за начало отсчета принимается период или дата, к которым относится срединный уровень ряда динамики. В рассматриваемом примере таким будет уровень 2008 г. Поэтому в графе 2 табл. 23.10 уровень 2008 г. принят за начало отсчета времени.
= 0, если за начало отсчета принимается период или дата, к которым относится срединный уровень ряда динамики. В рассматриваемом примере таким будет уровень 2008 г. Поэтому в графе 2 табл. 23.10 уровень 2008 г. принят за начало отсчета времени.
При четном числе уровней ряда динамики за начало отсчета времени также принимается середина изучаемого периода, а двум соседним периодам или датам в центре ряда присваиваются размеры 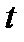 = -1 и
= -1 и 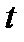 = 1, т. е. предполагается, что соседние уровни отстоят друг от друга во времени на
= 1, т. е. предполагается, что соседние уровни отстоят друг от друга во времени на  . Например, при четном числе уровней получим следующие значения t:
. Например, при четном числе уровней получим следующие значения t:
| Год | ||||||
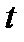
| -5 | -3 | -1 |
Следовательно, в данном случае время измеряется не в годах, а в полугодиях.
В обоих случаях  , в результате чего система нормальных уравнений (23.13) принимает вид
, в результате чего система нормальных уравнений (23.13) принимает вид
 ;
;
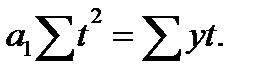
Тогда размеры параметров уравнения рассчитываются по формулам:  ;
; 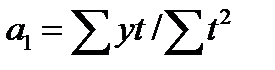 .
.
Подставив в эти уравнения, соответствующие размеры показателей (см. графы 3 и 4 табл. 23.9), получим:
 = 659,0/7 =94,14;
= 659,0/7 =94,14;
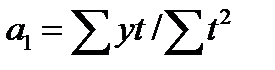 = (-44,1) /28 = -1,58.
= (-44,1) /28 = -1,58.
Отсюда следует, что уравнение прямой в рассматриваемом примере принимает вид: 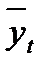 = 94,14-1,58
= 94,14-1,58 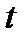 . Подставляя в это уравнение последовательно размеры
. Подставляя в это уравнение последовательно размеры 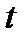 (графа 4, табл. 23.10) получим сглаженные размеры уровня погрузки для каждого года ряда динамики. Например для 2013 года расчет сглаженного размера погрузки будет иметь вид
(графа 4, табл. 23.10) получим сглаженные размеры уровня погрузки для каждого года ряда динамики. Например для 2013 года расчет сглаженного размера погрузки будет иметь вид 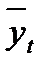 =94,14 -1,58 ∙(-3)=98,9 тыс. т.
=94,14 -1,58 ∙(-3)=98,9 тыс. т.
На рис. 23.4 графически изображены фактические данные о погрузке цветных металлов (эмпирический ряд динамики) и уровни, полученные на основе аналитического сглаживания.
Аналитическое сглаживание по уравнению прямой делает наглядным основное направление развития явления, а также дает представление о среднем размере скорости изменения уровней явления. Так, в рассматриваемом примере 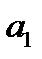 = 1,58 представляет собой среднегодовой размер прироста погрузки цветных металлов.
= 1,58 представляет собой среднегодовой размер прироста погрузки цветных металлов.
При аналитическом сглаживании ряда динамики по уравнению параболы второго порядка 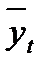 =
= 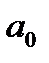 +
+  ,
,
система нормальных уравнений имеет следующий вид:

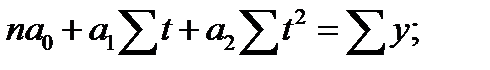
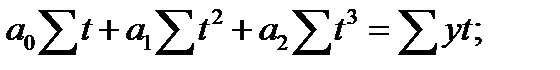
.
Если  (в этом случае
(в этом случае  ), система уравнений примет вид:
), система уравнений примет вид:
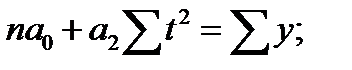
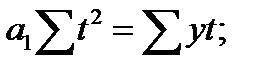
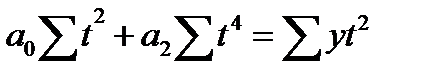 .
.
В дальнейшем определяются параметры уравнения и на основе полученного уравнения параболы второго порядка определяются сглаженные размеры уровней ряда динамики.
Результаты аналитического сглаживания могут быть использованы для интерполяции, т. е. для нахождения размеров показателя в пределах рассматриваемого периода, и для экстраполяции – нахождения размеров показателя за пределами рассматриваемого периода.
Для нахождения интерполируемых или экстраполируемых размеров показателя необходимо в аналитическое выражение уровня ряда поставить соответствующий размер 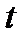 . Например, при нахождении ожидаемого размера погрузки цветных металлов в 2015 г. в уравнение примой следует поставить размер
. Например, при нахождении ожидаемого размера погрузки цветных металлов в 2015 г. в уравнение примой следует поставить размер 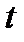 равный 4. Тогда предполагаемый уровень погрузки цветных металлов в филиале ООА « РЖД» может быть равен
равный 4. Тогда предполагаемый уровень погрузки цветных металлов в филиале ООА « РЖД» может быть равен 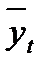 = 94,14-1,58∙4 =87,82 тыс. т.
= 94,14-1,58∙4 =87,82 тыс. т.
Поскольку при аналитическом сглаживании взаимно погашаются отклонения от подвижного среднего размера показателя, то сглаженные уровни ряда дают приближенную характеристику. Поэтому результаты интерполяции и экстраполяции надо использовать весьма аккуратно, не рассматривая их в качестве абсолютной истины.
Сезонные колебания и способы их измерения. Многочисленные явления общественной жизни подвержены ежемесячным, ежеквартальным или ежегодным периодическим колебаниям. Ежегодные периодические колебания называются сезонностью. Так, например, в летние и осенние месяцы возрастают перевозки грузов на железнодорожном транспорте, и соответственно их росту увеличивается потребность в подвижном составе. Периодическое уменьшение объема производства и, в некоторых случаях, даже его прекращение ведет к высвобождению рабочей силы и снижению загрузки основных средств. Поэтому изучение сезонности и ее количественная характеристика имеет важное значение.
Наиболее простым приемом выявления наличия сезонности является сопоставление месячных данных за ряд лет. Так, из сопоставления данных граф 2– 4 табл. 23.11 и рис. 23.5 видно, что увеличение среднемесячного отправления пассажиров на железной дороге, наблюдается ежегодно с июня по октябрь.
Для количественной характеристики интенсивности сезонных колебаний рассчитываются индексы сезонности. Существует несколько методов определения индексов сезонности, применяемых в зависимости от наличия исходных данных и характера колеблемости показателей во времени.
При наличии данных за один год индекс сезонности 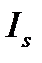 определяют отнесением данных за месяц
определяют отнесением данных за месяц  к среднемесячному размеру показателя за этот же год, т. е.
к среднемесячному размеру показателя за этот же год, т. е. 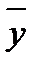 :
:
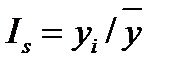 .(23.17)
.(23.17)
Результаты расчета индексов сезонности за каждый из 2012, 2013, и 2014 годов обобщены в графах 4,5.6.табл. 23.11.
При наличии данных за несколько лет индекс сезонности рассчитывается так: 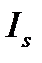 Is =
Is = 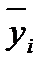 /
/  ,
,
где  i – средний размер показателя за одноименные месяцы;
i – средний размер показателя за одноименные месяцы;
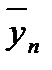 n. – средний размер показателя за период в целом.
n. – средний размер показателя за период в целом.
Результаты расчета индексов сезонности по данным за 2012-2014 годы обобщены в графе 7 табл. 23.11.
Таблица 23.11
Дата добавления: 2016-01-18; просмотров: 1277;
