Абсолютные показатели вариации
К числу абсолютных показателей вариации относят:
- размах вариации;
- среднее линейное отклонение;
- дисперсию;
- среднее квадратическое отклонение.
6.2.1.1 Размах вариации – это разность между максимальным и минимальным значениями признака.
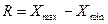 (6.1)
(6.1)
В наших примерах: R1 = 58 – 30 = 28 (дет.)
R2 = 48 – 40 = 8 (дет.)
Следовательно, для цеха № 2 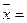 44 наиболее типична, чем для цеха № 1.
44 наиболее типична, чем для цеха № 1.
Преимущество данного показателя: простота его исчисления.
Недостатки:
1) он не учитывает внутреннюю колеблемость уровней ряда;
2) он часто зависит от случайности. Например, количество пропущенных часов занятий студентами группы,
Х, 4, 6, 8, 0, 8, 2, 4, 6, 8, 4, 0, 0, 80, 4, 8, 4, 6, 8, 8, 0, 0, 4, 2, 4, 2, 6
R= 80 – 0 = 80 час, хотя на самом деле за исключением одного студента вся остальная часть совокупности более-менее однородна по пропускам: 0 ÷ 8 час.
Область применения R поэтому ограничивается достаточно однородными совокупностями. Например, в предупредительном контроле качества продукции.
6.2.1.2 Среднее линейное отклонение – это средняя арифметическая величина, исчисленная из абсолютных отклонений индивидуальных значений признаков от средней величины.
Однако, учитывая нулевое свойство средней арифметической: сумма отклонений индивидуальных значений признака от средней равна 0. Поэтому при исчислении среднего линейного отклонения суммируются модули этих отклонений.
Т.е. формулы исчисления среднего линейного отклонения имеют вид:
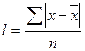 для простого вариационного ряда (для несгруппированных данных) либо
для простого вариационного ряда (для несгруппированных данных) либо
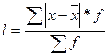 для дискретного ряда (для сгруппированных данных).
для дискретного ряда (для сгруппированных данных).
В наших примерах (все необходимые данные для расчетов будем получать в таблицах 6.1 и 6.2):
l1 = 320 / 40 = 8 (дет.)
l2 = 80 / 40 = 2 (дет.)
Преимущество среднего линейного отклонения перед размахом в том, что оно учитывает внутреннюю вариацию уровней ряда.
Недостаток: необходимо абстрагирование от знака отклонения, следовательно – трудности в применении математических методов анализа вариации.
Сфера практического использования: в текстильной промышленности для характеристики однородности толщины нитей и пряжи.
6.2.1.3 Дисперсия – наиболее распространенный в научной статистике показатель.
Дисперсия – это средняя из квадратов отклонений индивидуальных значений признака от его средней величины.
Она рассчитывается по формулам 6.2 и 6.3:
- для простого вариационного ряда
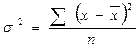 ; (6.2)
; (6.2)
- для дискретного ряда
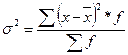 . (6.3)
. (6.3)
В наших примерах:
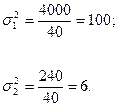
Дисперсия может быть исчислена и другим способом: как разность между средней из квадратов индивидуальных значений признака и квадратом средней величины, т.е.
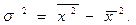 (6.4)
(6.4)
Тогда для простого вариационного ряда формула дисперсии принимает вид:
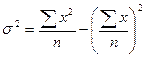 , (6.5)
, (6.5)
а для дискретного
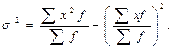
(6.6)
В нашем примере:
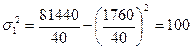 ;
;
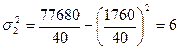 .
.
Результаты получаются одинаковые, независимо от применяемой формулы.
Исчисление дисперсии можно упростить, используя для этих целей ее математические свойства (см. 6.3).
Недостаток этого показателя вариации – его размерность. Размерность дисперсии равна квадрату размерности изучаемого признака. Этот недостаток устраняется при переходе к среднему квадратическому отклонению.
6.2.1.4 Среднее квадратическое отклонение определяется как квадратный корень из среднего квадрата отклонений индивидуальных значений признака от их средней величины, т.е.:
- для простого вариационного ряда
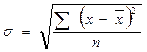 ; (6.7)
; (6.7)
- для дискретного ряда
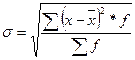 . (6.8)
. (6.8)
Следовательно, если дисперсия уже исчислена, среднее квадратическое отклонение рассчитывается извлечением квадратного корня из дисперсии:
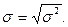
(6.9)
В наших примерах:
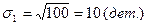
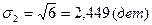
Возведение 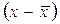 в квадрат, а затем извлечение квадратного корня позволяет избежать воздействия нулевого свойства средней арифметической.
в квадрат, а затем извлечение квадратного корня позволяет избежать воздействия нулевого свойства средней арифметической.
Среднеквадратическое отклонение (в иностранной литературе – стандартное отклонение) является общепринятым показателем не только в статистике, но и в технике, в биологии и др. областях знаний.
Между средним линейным и средним квадратическим отклонением в распределениях, близких к нормальному, существует следующее примерное соотношение: 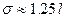 .
.
Дата добавления: 2016-01-16; просмотров: 2552;
