СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВАРИАЦИИ
6.1. Понятие вариации и необходимость её статистического изучения.
6.2. Показатели вариации.
6.2.1 Абсолютные показатели вариации.
6.2.2 Относительные показатели вариации.
6.3. Дисперсия, её виды и свойства.
6.1 Понятие вариации и необходимость её статистического изучения
Вариацией признака называется его изменение при переходе от одной единицы наблюдения к другой.
С другой стороны, вариация – это то, что порождает необходимостьстатистики. Как уже отмечалось ранее, лишено смысла исследование стоимости автобусного билета в городе Витебске, так как это явление не варьирующее.
После того, как исчислена средняя величина, возникает вопрос о её надёжности или её типичности. При этом необходимо учитывать, что типичность средней находится в обратной зависимости от вариации (колеблемости) уровней признака: чем больше вариация уровней исходной информации, тем меньше типичность (представительность, репрезентативность) средней величины. В случае слишком большой вариации уровней ряда можно получить фиктивную среднюю.
Рассмотрим два примера, в которых уровни средних величин равны, но эти средние имеют разные представительности.
Пример: имеется информация о выработке рабочих двух цехов.
Таблица 6.1 – Распределение рабочих цеха № 1 по уровню выработки деталей в смену
| Выработка 1 рабочего в смену, дет x | Число рабочих, чел f | xf | 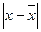
| 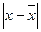 f f
| 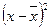
| 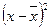 f f
| x2 | x2f |
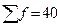
| 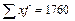
| 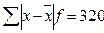 = 320 = 320
| 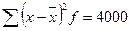 =4000 =4000
| 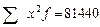
|
Таблица 6.2 – Распределение рабочих цеха № 2 по уровню выработки деталей в смену
| Выра-ботка 1 рабочего в смену, дет x | Число рабочих, чел. f | xf | 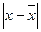
| 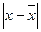 f f
| 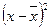
| 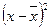 f f
| x2 | x2f |
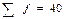
| 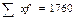
| 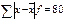
| 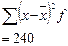
| 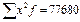
|
В обоих случаях средняя выработка рассчитывается по формуле средней арифметической взвешенной:
Цех № 1 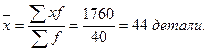
Цех № 2 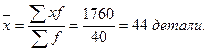
Однако, анализируя уровни исходной информации, замечаем:
Цех №1 − вариация выработки от 30 до 58 деталей в смену.
Цех №2 − вариация выработки от 40 до 48 деталей в смену.
Следовательно, 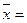 44 наиболее типична для цеха № 2.
44 наиболее типична для цеха № 2.
Для характеристики степени вариации признака (а следовательно, для оценки типичности средней величины) в статистике используют следующие показатели:
1) размах вариации (R);
2) среднее линейное отклонение (l);
3) дисперсия ( 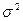 );
);
4) среднее квадратическое отклонение ( 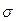 );
);
5) коэффициент осцилляции (Кr);
6) относительное линейное отклонение (Кl);
7) коэффициент вариации (V);
Первые четыре относятся к абсолютным показателям вариации, а последние три − к относительным.
Значение показателей вариации заключается в следующем:
1) они дополняют средние величины, за которыми скрываются индивидуальные различия отдельных единиц совокупности;
2) они характеризуют степень однородности статистической совокупности по изучаемому признаку;
3) они характеризуют границы вариации признака;
4) соотношение показателей вариации может быть использовано для характеристики взаимосвязи между признаками (см. 6.3).
Дата добавления: 2016-01-16; просмотров: 1150;
