Свойства средней арифметической величины и их практическое использование
Наиболее распространённым видом средних величин является средняя арифметическая. Она обладает рядом математических свойств, значение которых не только позволяет понять сущность средних, но и позволяет упростить расчёт средней величины (особенно в тех случаях, когда значения признака имеют достаточно громоздкий вид).
К основным математическим свойствам средней величины относятся следующие:
1. Произведение средней величины на сумму всех частот равно сумме произведений индивидуальных значений признака на соответствующие частоты (свойство вытекает из формулы 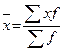 ):
):
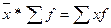 . (5.13)
. (5.13)
2. Сумма отклонений индивидуальных значений признака от средней величины равна 0:
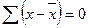 − для несгруппированных данных;
− для несгруппированных данных;
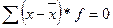 − для сгруппированных данных.
− для сгруппированных данных.
3. Сумма квадратов отклонений индивидуальных значений признака от средней величины меньше суммы квадратов их отклонений от любой другой постоянной величины (х0):
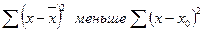 − для несгруппированных данных;
− для несгруппированных данных;
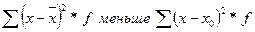 − для сгруппированных данных.
− для сгруппированных данных.

4. Средняя арифметическая суммы варьирующих величин равна сумме средних арифметических этих величин:
если xi = yi + zi, то 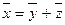 .
.
Доказательство:
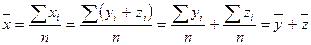 . (5.14)
. (5.14)
5. Если все варианты ряда уменьшить (увеличить) в А раз, то средняя уменьшается (увеличивается) в А раз.
Это означает, что 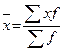 можно исчислять как
можно исчислять как 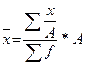 либо
либо 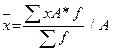 .
.
6. Если все варианты ряда уменьшить (увеличить) на одно и то же число х0, то и средняя величина уменьшиться (увеличиться) на х0, то есть 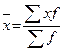 может быть рассчитана как
может быть рассчитана как 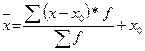 либо
либо 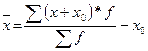 .
.
7. Если все частоты ряда разделить (умножить) на одно и то же число b, то средняя не изменится, то есть 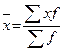 может быть рассчитана как
может быть рассчитана как 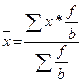 либо как
либо как 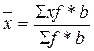
Последние три свойства из перечисленных могут использоваться одновременно для упрощения расчетов, и тогда считается, что средняя рассчитывается по «способу моментов» или «методом отсчета от условного нуля». В данном случае важен факт правильного выбора А (чаще всего это величина интервала) и х0 (чаще всего это середина какого-либо интервала).
Исчисление средней по «способу моментов» производится по формуле, вид которой меняется в зависимости от порядка применения свойств:
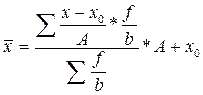 (5.15)
(5.15)
либо 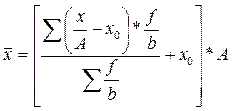
и т.д.
Независимо от того, применяются либо не применяются свойства средней величины, результат расчета средней остается неизменным.
Например, необходимо определить среднюю заработную плату работников организации, в т.ч. по «способу моментов».
Таблица 5.9 – Расчет средней заработной платы
| ЗП, тыс. руб., х | Число раб-ков, f | x | xf | x-x0 (x0=1300) | 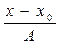 (A=200) (A=200)
| 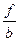 (b=20)
(b=20)
| 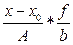
|
| 800 − 1000 1000 −1200 1200 −1400 1400 −1600 1600 −1800 1800 − 2000 | -400 -200 | -2 -1 | -2 -4 | ||||
| Σf=400 | Σ xf= | Σ 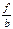 =20 =20
| Σ 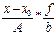 =5 =5
|
Без использования свойств средней величины:
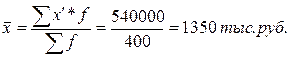
С использованием свойств средней величины:
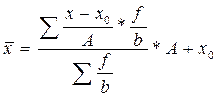
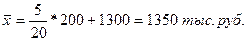
Дата добавления: 2016-01-16; просмотров: 1466;
