Дисперсия, ее виды и свойства
Вариация признака складывается под воздействием множества факторов, т.к. социально-экономические явления и процессы носят сложный характер. В исследованиях иногда возникает необходимость оценить не только общую вариацию признака, но и ту ее часть, которая обусловлена действием постоянных, стабильных, а не случайных факторов. В этих случаях рассчитывают три вида дисперсии:
- общую;
- межгрупповую;
- внутригрупповую.
Общая дисперсия характеризует общую вариацию признака под влиянием всех факторов (условий, причин). Она рассчитывается по формуле 6.13:
 , (6.13)
, (6.13)
где 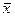 − средняя по всей изучаемой совокупности.
− средняя по всей изучаемой совокупности.
Для определения влияния постоянного фактора на вариацию признака производят аналитическую группировку, в основании которой лежит данный фактор. Вариация, обусловленная фактором, положенным в основание группировки, оценивается с помощью межгрупповой дисперсии:
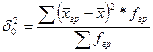 , (6.14)
, (6.14)
где 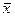 гр – средняя по отдельным группам;
гр – средняя по отдельным группам;
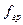 − численность отдельных групп.
− численность отдельных групп.
Для определения влияния случайных факторов рассчитывают дисперсию внутри каждой группы, т.е. внутригрупповую
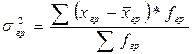 , (6.15)
, (6.15)
где xгр – индивидуальные значения признака в группе,
fгр – их частоты;
а затем среднюю из внутригрупповых дисперсий

(6.16)
Доказано, что общая дисперсия равна сумме межгрупповой дисперсии и средней из внутригрупповых дисперсий:
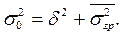
(6.17)
Это равенство называется правилом сложения дисперсий.
Правило сложения дисперсий получило широкое распространение на практике. На его основе вычисляется эмпирическое корреляционное отношение (коэффициент корреляционного отношения или эмпирический коэффициент корреляционного отношения):
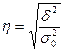 принимает значение от 0 до 1.
принимает значение от 0 до 1.
Оно показывает тесноту связи между признаками (раздел 10).
Возведенное в квадрат эмпирическое корреляционное отношение представляет собой коэффициент детерминации ( 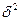 ), который характеризует долю общей колеблемости признака-результата, вызванную действием признака-фактора, положенного в основание группировки.
), который характеризует долю общей колеблемости признака-результата, вызванную действием признака-фактора, положенного в основание группировки.
Наряду с вариацией количественного признака часто возникает необходимость измерить вариацию альтернативного признака.
Если ввести обозначения:
1 – наличие интересующего исследователя признака;
0 – отсутствие интересующего исследователя признака;
p – доля единиц, обладающих данным признаком;
q – доля единиц, не обладающих данным признаком,
то среднее значение альтернативного признака будет равно:
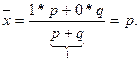
(6.18)
Тогда дисперсия альтернативного признака определяется по формуле

 . (6.19)
. (6.19)
Учитывая, что 1− p = q
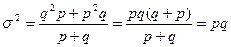 . (6.20)
. (6.20)
Таким образом, дисперсия альтернативного признака равна произведению доли единиц, обладающих данным признаком, на долю единиц, которые им не обладают:
 либо
либо 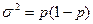 . (6.21)
. (6.21)
Дисперсия облает рядом математических свойств, которые значительно упрощают её вычисление. К основным из них относятся следующие:
1. Если все значения признака увеличить или уменьшить в А раз, то дисперсия соответственно увеличится или уменьшится в 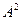 раз.
раз.
2. Если все значения признака увеличить или уменьшить на какое-то постоянное число x0, то дисперсия от этого не изменится.
3. Если все значения частот различить или умножить на какое-то число b, то дисперсия от этого не изменится.
Используя эти свойства одновременно, можно рассчитать дисперсию по «способу моментов». Если взять за основу исходную формулу дисперсии
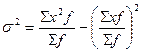 , (6.22)
, (6.22)
то формула дисперсии, исчисляемой по «способу моментов», будет иметь вид:
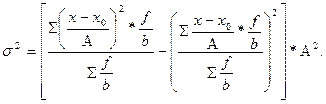
(6.23)
Например, рассчитаем дисперсию выработки рабочих цеха № 2 по «способу моментов» (таблица 6.3).
Таблица 6.3 – Расчет дисперсии выработки по «способу моментов»
| x | f | 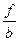 b=5
b=5
| 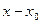
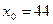
|  A=2 A=2
| 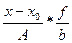
| 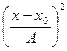
| 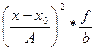
|
| -4 -2 | -2 -1 | -2 -2 | |||||
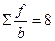
| 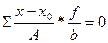
| 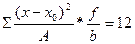
|
Исходя из полученных данных:
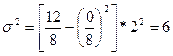 .
.
Таким образом, результат не зависит от применяемой формулы. В нашем примере (цех № 2) по всем формулам (6.3, 6.6, 6.23) получено одно и то же значение дисперсии 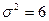 .
.
Дата добавления: 2016-01-16; просмотров: 2133;
