Обобщающие характеристики генеральной и выборочной совокупности

Генеральной совокупностью называется вся изучаемая совокупность единиц. Например, при изучении общественного мнения студентов УО «ВГТУ» – это все студенты УО «ВГТУ».

Численность генеральной совокупности обозначается в статистике N.

Выборочная совокупность – это та часть единиц генеральной совокупности, которая подвергается выборочному обследованию.

Численность выборочной совокупности обозначается n. Например, n при изучении общественного мнения – это число опрошенных студентов УО «ВГТУ».

Как уже отмечалось, задача выборочного наблюдения состоит в том, чтобы на основе изучения выборочной совокупности получить правильное представление о показателях генеральной совокупности.

В том случае, когда исследование проводится по количественному признаку, в качестве обобщающей характеристики совокупности применяется среднее значение (средняя величина, средний размер) признака.

Среднее значение варьирующего признака по всей совокупности называется генеральной средней и определяется как:

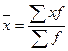и при этом 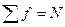. (7.1)

Среднее значение признака у единиц, которые подверглись выборочному обследованию, называется выборочной средней и определяется по формуле

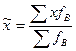, в свою очередь, 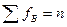. (7.2)

В данном случае задача выборочного наблюдения состоит в том, чтобы на основе выборочной средней 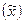дать правильное представление о генеральной средней .

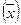Для характеристики совокупности по альтернативно варьирующему признаку в качестве обобщающего показателя используется доля (частость).

Доля определяется по генеральной совокупности и характеризует ту часть единиц генеральной совокупности, которая обладает признаком, интересующим исследователя. Обозначается латинской буквой p.

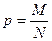, (7.3)

где M – число единиц генеральной совокупности, обладающих интересующим исследователя признаком.

В свою очередь:

q = 1 – p – это доля единиц, не обладающих данным признаком.

Например, из 8000 студентов УО «ВГТУ» 6000 посещают университетскую столовую.

Тогда их доля составит (N = 8000, M = 6000):

.

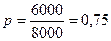Выборочная доля, или доля в выборочной совокупности, называется частостью и определяется как отношение:

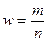, (7.4)

где m – число единиц выборочной совокупности, обладающих интересующим исследователя признаком.

Например, выборочно обследовано 200 студентов, и из них 145 посещают столовую (n = 200, m = 145):

.

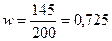В случае альтернативного признака задача выборочного наблюдения состоит в том, чтобы на основе определения частости дать верное представление о доле в генеральной совокупности.

Кроме среднего размера признака и доли для характеристики генеральной и выборочной совокупности, могут быть использованы:

- генеральная и выборочная дисперсии;

- генеральное и выборочное среднее квадратическое отклонение;

- другие статистические характеристики.

Таблица 7.1 – Обобщающие характеристики генеральной и выборочной совокупности

Показатели	Совокупность
генеральная	выборочная
Объём (число единиц) совокупности	N	N
Среднее значение признака
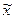
Число единиц, обладающих изучаемым признаком	M	m
Доля единиц, обладающих изучаемым признаком	p	w
Доля единиц, не обладающих изучаемым признаком	1-p (q)	1-w
Дисперсия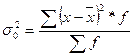
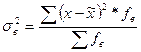
Среднее квадратическое отклонение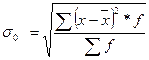

Расхождения между генеральными и выборочными характеристиками изучаются на основе предельных теорем теории вероятности.

В статистике речь идёт о возможных ошибках выборки.