Малая выборка и сфера ее применения

Несмотря на то, что уменьшение объема выборки сопровождается ростом величины стандартной ошибки, на практике часто приходится ограничиваться малым числом наблюдений. Чаще всего эта необходимость возникает при проверке качества продукции, связанной с ее уничтожением (так называемый разрушающий контроль качества продукции). Например, при проверке ткани на разрыв.

В этих случаях ограничиваются малыми выборками.

Под малой выборкой понимается такое выборочное наблюдение, численность единиц которого не превышает 30 единиц.

Первые работы в теории малых выборок были проведены Стьюдентом и продолжены Фишером. Доказано, что и при малых выборках характеристики выборочной совокупности могут быть перенесены на генеральную совокупность. Однако расчет средней и предельной ошибок в случае малой выборки имеет свои особенности.

В математической статистике доказано, что соотношение между выборочной и генеральной дисперсией:

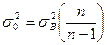. (7.30)

В случае достаточно большого объема выборки сомножителем 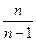пренебрегают, т.к. 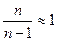(см. 7.4).

Однако в случае малой выборки этого делать нельзя. Тогда формула средней ошибки малой выборки будет иметь вид:

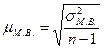. (7.31)

Вывод формулы:

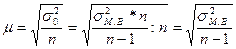. (7.32)

Предельная ошибка малой выборки

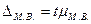. (7.33)

Однако величина t иначе связана с вероятностной оценкой, чем при обычной выборке. В данном случае вероятностная оценка зависит не только от t, но и от n.

Таблица 7.3 – Распределение вероятности ошибок в зависимости от коэффициента доверия и численности малых выборок (фрагмент)

n t		…		…		…	Обычная выборка
… … …	0,626   0,884   0,960		0,657   0,924   0,984		0,670   0,940   0,992		0,683   0,954   0,997

Как и в случае обычной выборки, на заключительном этапе определяются доверительные интервалы, в которых может находиться генеральная средняя

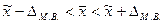(7.34)

или генеральная доля

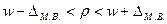. (7.35)