Показатели и способы оценки влияния структуры на динамику средних размеров показателей.
Для оценки влияния структуры на средние уровни показателей в динамике используется система показателей: индексы переменного состава, постоянного состава и структурных сдвигов. Система этих индексов строится на основе предположения причинно-следственной связи, которая якобы существует между средним размером показателя, структурой единиц совокупности и размером показателя по группам единиц. Такая взаимосвязь возникает в силу использования в процессе анализа средних размеров показателей, которые в зависимости от имеющихся исходных данных могут быть средними арифметическими взвешенными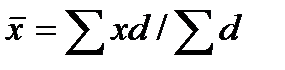 
или средними гармоническими взвешенными 
.
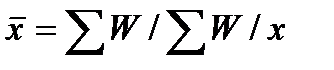Так, причинно-следственная взаимосвязь первого типа существует, например, между средним размером продолжительности простоя вагона под определенной технологической операцией, продолжительностью простоя по типам вагонов и структурой числа простоев по типам вагонов. Взаимосвязь второго типа существует между средним размером статической нагрузки вагона, структурой массы погруженных грузов и статической нагрузкой вагона по родам грузов.
Соотношение средних уровней показателей за текущий и базисный периоды, характеризующее их динамику называется индексом переменного состава. Этот индекс отражает совместное влияние на динамику среднего размера показателя изменения размеров осредняемого показателя и структуры совокупности.
При первой форме связи индекс переменного состава определяется по формуле:
I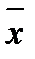 
= 
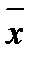1 / 
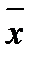0 , =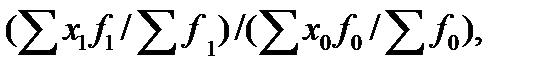 
,
где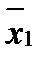
, 
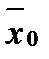– средний размер показателя соответственно в текущем и в базисном периодах;
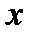– осредняемый показатель);
– частота повторения размеров осредняемого показателя.
В том случае когда вместо частоты повторения размеров показателей, выраженной числом единиц совокупности, обладающих определенным размером, имеются их доли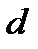 
, т. е. частости повторения размеров осредняемого показателя формула индекса переменного состава принимает вид
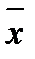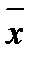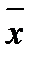I = 1 / 0 , =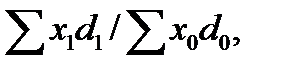 
, (23.1)
Относительное влияние изменения размеров осредняемого показателя на динамику среднего размера показателя определяется при помощи индекса постоянного состава, порядок расчета которого имеет следующий вид
= 
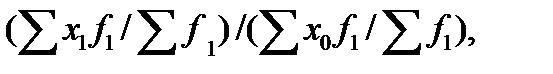
а при наличии данных о доле единиц совокупности обладающих конкретными размерами показаателя формула принимает вид:
= 
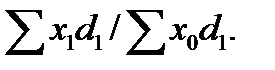. (23.2)
Относительное влияние изменения структуры совокупности на динамику среднего размера показателя определяется с помощью индекса структурных сдвигов, рассчитываемого в зависимости от имеющихся в наличии данных по формулам:
= 
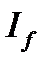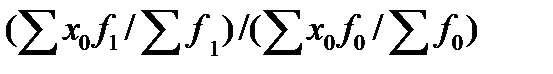или
= 
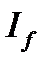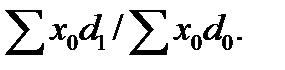(23.3)
Из формул (23.2) и (23.3) видно, что при определении индекса постоянного состава исключается влияние изменения структуры совокупности на динамику среднего размера показателя, а при определении индекса структурных сдвигов – влияние на него изменения размеров осредняемых показателей.
Рассмотрим применение формул (23.1), (23.2) и (23.3) при анализе динамики средней дальности перевозки пассажиров (табл. 23.1).
Средняя дальность перевозки пассажиров определяется на основе деления пасажирооборота на количество перевезенных пассажиров. Следовательно, уровень средней дальности перевозки пассажиров зависит от дальности перевозки пассажиров по видам сообщения и структуры перевезенных пассажиров по видам сообщения. Таким образом, между ними имеется причинно-следственная связь первого типа.
Таблица 23.1
Динамика дальности и структуры пассажирских перевозок по видам сообщения (данные условные)
| Вид сообщения | Базисный период | Текущий период | Индексы средней дальности перевозки | ||
| Средняя дальность перевозки, км | Удельный вес перевезенных пассажиров, % | средняя дальность перевозки, км | Удельный вес перевезенных пассажиров, % | ||
| Пригородное Дальнее | 38,9 860,2 | 89,4 10,6 | 41,1 862,8 | 89,9 10,1 | 1,057 1,003 |
| Итого | 126,0 | 100,0 | 124,1 | 100,0 | 0,985 |
Индекс переменного состава, рассчитанный по формуле (23.1) равен I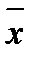 
=124,1/126,0= 0,985, или 98,5%. Это означает, что средняя дальность перевозки пассажиров в текущем периоде по сравнению с базисным периодом снизилась на 1,5%.
Дальность перевозки пассажиров за рассматриваемый период увеличилась в пригородном сообщении на 41,1-38,9=2,2 км, а в дальнем следовании на 862,8- 860,2=2,6 км. Следовательно, влияние этого фактора должно было вызвать увеличение средней дальности перевозки пассажиров.
Удельный вес пассажиров, перевезенных в пригородном сообщении, увеличился с 89,4 до 89,9%, а удельный вес пассажиров, перевезенных в дальнем следовании, уменьшился с 10,6 до 10,1 %. Поскольку средняя дальность перевозки пассажиров в дальнем следовании в базисном периоде составляла 860,2 км, а в пригородном только 38,9 км, то увеличение удельного веса перевезенных пассажиров в пригородном сообщении на 0,5 % должно привести к сокращению средней дальности перевозок пассажиров. В результате совместного влияния указанных причин средняя дальность сократилась на 1,9 км (124,1-126,0).
Следовательно, влияние изменения структуры перевозок пассажиров на среднюю дальность их перевозки было сильнее, чем влияние изменения дальности перевозок пассажиров по видам сообщения.
Ситуация, когда средний размер показателя уменьшается (увеличивается), несмотря на увеличение (уменьшение) размеров осредняемого показателя, называется статистическим парадоксом. Из рассмотренного примера следует, что статистический парадокс обусловливается влиянием изменения структуры совокупности.
Относительное влияние на среднюю дальность перевозок пассажиров изменения структуры определяется на основе индекса структурных сдвигов (23.3):
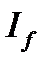= [(38,9٠89,9+860,2٠10,1) ] / [(38,9٠89,4+860,2٠10,6) /100= =121,9/126,0 = 0,967, или 96,7%.
Абсолютное изменение средней дальности перевозки пассажиров в результате изменения структуры перевозок по видам сообщения рассчитывается как разница между числителем и заменателем индекса структурных сдвигов
∆ 
= 121,9-126,0=-4,1 км.
Следовательно, увеличение доли перевозки пассажиров в пригородном сообщении, т. е. перевезенных на более короткое расстояние, привело к сокращению средней дальности перевозки пассажиров на 3,3 % или на 4,1 км.
Относительное влияние на среднюю дальность изменения дальности перевозки пассажиров по видам сообщения определяется по формуле
= [(41,1٠89,9+862,8٠10,1)/100]/[(38,9٠89,9+860,2٠10,1) /100] = =124,1/121,9 = 1,018 или 101,8%.
Индекс постоянного состава = 101,8%, указывает на то, что увеличение дальности перевозки пассажиров в пригородном сообщении на 5,7% и в дальнем следовании на 0,3% привело к росту средней дальности перевозки пассажиров на 1,8 %.
Абсолютный прирост средней дальности перевозки пассажиров, обусловленный изменением размеров осредняемого показателя, определяется как разница между числителем и знаменателем индекса постоянного состава
D 
= 124,1-121,9=2,2 км.
Таким образом, средняя дальность перевозки пассажиров в связи с измененем дальности перевозок пассажиров по видам сообщений возросла на 1,8% или на 2,2 км.
Проверка правильности расчетов может быть осуществлена путем использования формулы взаимосвязи индексов переменного состава, постоянного состава и структурных сдвигов:
I 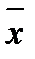= = 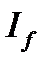1,018∙0,967=0,985 или 98,5%.
В том случае, когда взаимосвязь между средним размером показателя, структурой единиц носителей показателя и размерами показателя по группам выражается формулой средней гармонической взвешенной, система индексов переменного, постоянного состава и структурных сдвигов несколько преобразуется.
Рассмотрим это на примере анализа динамики средней статической нагрузки вагона (табл. 23.2). Средняя статическая нагрузка вагона зависит от размера статической нагрузки вагона по родам грузов и структуры массы погруженных грузов по их родам. Характеристику изменения среднего размера статической нагрузки вагона дает индекс переменного состава расчет, которого можно произвести по формуле:
I 
= 1/ 0 .
Средние размеры статической нагрузки вагона в базисном и текущем периодах определяются как средние гармонические взвешенные и их расчет принимает следующий вид:
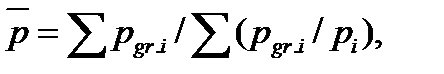
где ,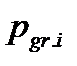 
—масса грузов i-го вида погруженных в вагоны, т.
Таблица 23.2
Дата добавления: 2016-01-18; просмотров: 1050;