Всестороннее сжатие
Запишем выражение для давления при упругой деформации
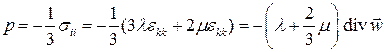 .
.
Введем модуль объемной упругости
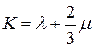 .
.
Тогда
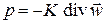 .
.
Видим, что модуль объемной упругости 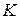 характеризует сопротивление объемному сжатию.
характеризует сопротивление объемному сжатию.
Иногда используют обратную величину
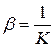
– коэффициент сжимаемости.
Тогда
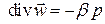 .
.
Сдвиг
Напряжение и деформация сдвига описываются недиагональными элементами тензоров деформаций и напряжений.
По закону Гука
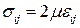 ,
, 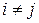 .
.
Это выражение напоминает закон течения ньютоновской жидкости, но вместо 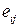 стоит
стоит 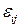 .
.
Коэффициент 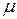 называется модулем сдвига и обозначается
называется модулем сдвига и обозначается 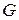
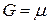 .
.
В теории упругости пользуются парами коэффициентов упругости: 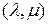 , или
, или 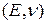 , или
, или 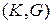 . Эти коэффициенты выражаются друг через друга следующим образом
. Эти коэффициенты выражаются друг через друга следующим образом
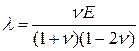 ,
, 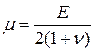 ,
,
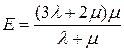 ,
, 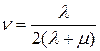 ,
,
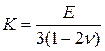 ,
, 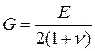 ,
,
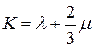 ,
, 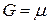 .
.
Все модули неотрицательные, поэтому 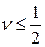 .
.
Видно, что 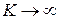 при
при 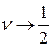 , поэтому
, поэтому 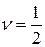 соответствует несжимаемому материалу.
соответствует несжимаемому материалу.
Из закона Гука следует выражение для упругих деформаций через напряжения
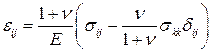 .
.
Уравнения акустики
Уравнения акустики
Акустика изучает распространение звука или малых возмущений в сплошной среде. Уравнения акустики можно получить линеаризацией уравнений гидродинамики.
Как было показано выше, уравнения динамики идеальной жидкости имеют вид
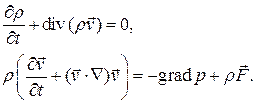
Если считать течение баротропным, то есть
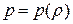 ,
,
то система уравнений замкнута.
Пусть 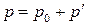 ,
, 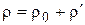 и
и 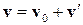 . Здесь индексом 0 отмечены значения давления, плотности и скорости, усредненные по большому промежутку времени, и постоянные или начальные значения; а штрихом – возмущения этих величин. Предположим, что возмущения
. Здесь индексом 0 отмечены значения давления, плотности и скорости, усредненные по большому промежутку времени, и постоянные или начальные значения; а штрихом – возмущения этих величин. Предположим, что возмущения 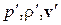 малы по сравнению с
малы по сравнению с 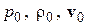 . В рамках этого предположения получим уравнения для распространения малых возмущений, т.е. уравнения акустики. Будем сохранять лишь члены с возмущениями в первой степени. Тем самым линеаризуем уравнения гидродинамики. Разлагая в ряд Тейлора уравнение состояния , получим
. В рамках этого предположения получим уравнения для распространения малых возмущений, т.е. уравнения акустики. Будем сохранять лишь члены с возмущениями в первой степени. Тем самым линеаризуем уравнения гидродинамики. Разлагая в ряд Тейлора уравнение состояния , получим
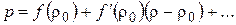 ,
,
или
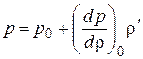 .
.
По определению 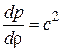 , где
, где 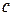 называется скоростью звука в среде. Тогда
называется скоростью звука в среде. Тогда
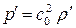 .
.
Линеаризованное уравнение состояния называется акустическим уравнением состояния.
Предположим отсутствие поступательного движения, общего для всех точек сплошной среды, т.е. 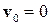 . Это предположение не ограничивает общности, так как можно перейти к системе координат, движущейся поступательно со скоростью
. Это предположение не ограничивает общности, так как можно перейти к системе координат, движущейся поступательно со скоростью 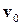 , в которой жидкость будет покоиться.
, в которой жидкость будет покоиться.
Линеаризуем уравнение неразрывности
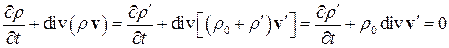 .
.
Линеаризуем уравнение импульсов
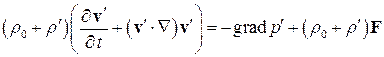 .
.
В отсутствие внешних массовых сил 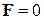 . Оставляя члены первого порядка, получим линеаризованное уравнение сохранения импульса
. Оставляя члены первого порядка, получим линеаризованное уравнение сохранения импульса
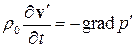 .
.
Выпишем замкнутую систему уравнений акустики - :
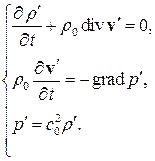
Дата добавления: 2015-12-29; просмотров: 1287;
