Уравнения Навье-Стокса
Уравнением Навье-Стокса называют уравнение импульсов ньютоновской жидкости. Имея в виду три скалярных уравнения, принято говорить уравнения Навье-Стокса.
Подставив в уравнение импульсов
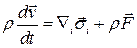
выражение 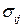 из уравнения состояния для ньютоновской жидкости , можно получить уравнение Навье-Стокса
из уравнения состояния для ньютоновской жидкости , можно получить уравнение Навье-Стокса
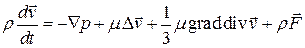 .
.
Проделаем выкладки.
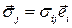 ,
,
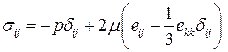 ,
,
 .
.
Первое слагаемое дает градиент давления с обратным знаком. Второе слагаемое
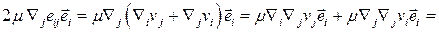
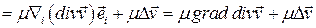 .
.
Третье слагаемое
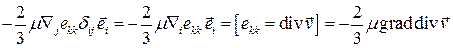 .
.
Таким образом,
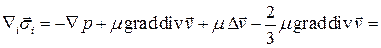
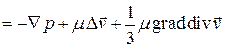 .
.
Подставим это выражение в уравнение импульсов и получим уравнение Навье-Стокса
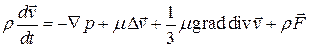
Если жидкость несжимаемая, то уравнение упрощается и принимает вид
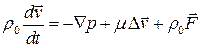 .
.
В пределе, когда 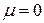 , получим уравнение импульсов идеальной жидкости
, получим уравнение импульсов идеальной жидкости
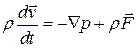 .
.
Течение Куэтта
Течением Куэтта называется плоское стационарное течение вязкой несжимаемой жидкости между двумя бесконечными пластинами (Рис. 3.1.4), одна из которых неподвижна, а другая движется с постоянной скоростью  . При этом расстояние
. При этом расстояние 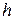 между пластинами остается постоянным, а внешние силы отсутствуют.
между пластинами остается постоянным, а внешние силы отсутствуют.
Математическая постановка задачи Куэтта включает уравнения неразрывности и импульсов
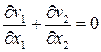 ,
,
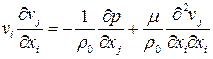 ,
, 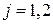 ,
,
и граничные условия, которые выражают условие прилипания жидкости к пластинам:

Можно убедиться, что решением задачи является:
 ,
, 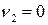 ,
, 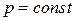 .
.
Течение Куэтта является слоистым или ламинарным, то есть жидкость перемещается слоями, параллельными направлению течения (lamina - пластина, полоса). Зная скорость, можно вычислить компоненты тензора вязких напряжений:
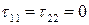 ,
, 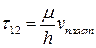 .
.
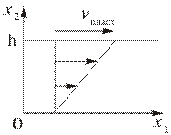 Рис. 3.1.4
Рис. 3.1.4
| Таким образом, на каждую единичную площадку, перпендикулярную оси 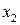 (Рис. 3.1.4), действует постоянное сопротивление вязкого трения, направленное против движения жидкости. (Рис. 3.1.4), действует постоянное сопротивление вязкого трения, направленное против движения жидкости.
|
Течение Пуазейля
Течением Пуазейля называется стационарное ламинарное течение вязкой несжимаемой жидкости через трубу круглого поперечного сечения под действием заданного перепада давления, причем движение жидкости во всех сечениях одинаково.
Математическая модель течения Пуазейля выглядит следующим образом
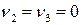 ,
, 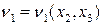 .
.
Уравнение неразрывности превращается в тождество, а уравнение Навье-Стокса имеет вид
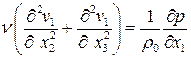 ,
, 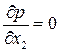 ,
,  .
.
Причем 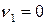 при
при 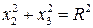 и
и
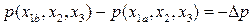 , при
, при 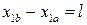 ,
,
где 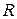 – радиус трубы,
– радиус трубы, 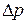 – заданный перепад давления на расстоянии
– заданный перепад давления на расстоянии 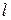 . Задача Пуазейля имеет точное решение. Найдем его. Из уравнений следует, что
. Задача Пуазейля имеет точное решение. Найдем его. Из уравнений следует, что
 , т.е.
, т.е.  ,
, 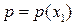 ,
,
причем эта зависимость линейная. Поэтому из граничного условия на давление и из вида решения следует, что
 .
.
Таким образом, задача сводится к задаче для 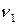

Можно убедиться, что решением задачи является функция
 ,
, 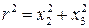 .
.
Согласно найденному решению скорость потока в сечении изменяется в зависимости от радиуса r по параболическому закону, достигая максимума на оси трубы.
Вычислим объемный расход жидкости Q через сечение трубы S (формула Пуазейля)
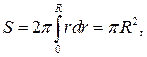
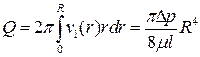 ,
, 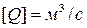 .
.
Среднюю (среднеобъемную) скорость потока можно определить следующим образом
 .
.
Видно, что
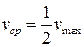 .
.
Можно ввести коэффициент сопротивления трубы 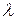 как отношение силы сопротивления к скоростному напору и площади контакта жидкости с трубой
как отношение силы сопротивления к скоростному напору и площади контакта жидкости с трубой
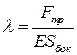 .
.
Рассмотрим жидкий цилиндр длины l, движущийся со средней скоростью 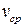 . Тогда площадь контакта
. Тогда площадь контакта 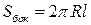 , скоростной напор
, скоростной напор 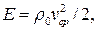 сила сопротивления трения со стороны трубы
сила сопротивления трения со стороны трубы 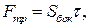 напряжение сдвига
напряжение сдвига 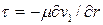 при
при 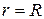 . В результате вычислений получим
. В результате вычислений получим  , т.е. сила сопротивления уравновешивает силу, движущую жидкий цилиндр за счет перепада давления.
, т.е. сила сопротивления уравновешивает силу, движущую жидкий цилиндр за счет перепада давления.
Введемчисло Рейнольдса 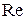 , которое определяется формулой
, которое определяется формулой
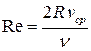 .
.
Тогда для течения Пуазейля коэффициент сопротивления выражается через число Рейнольдса и равен
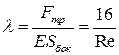 .
.
Закон Пуазейля справедлив для ламинарных (слоистых) течений, которые наблюдаются при малых числах Рейнольдса, когда трубка очень тонкая или жидкость очень вязкая.
Дата добавления: 2015-12-29; просмотров: 2453;
