Потенциальное течение идеальной несжимаемой жидкости

Покажем, что потенциальное течение идеальной несжимаемой жидкости описывается одним уравнением.

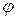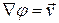По определению потенциального течения существует такая функция , что . Запишем уравнение неразрывности для несжимаемой жидкости

.

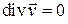Выразив скорость течения через потенциал, получим уравнение Лапласа относительно потенциала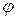

.

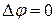Рассмотрим задачу Неймана для уравнения Лапласа:

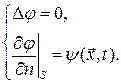
Выясним физический смысл задачи Неймана.

Пусть абсолютно твердое тело с поверхностью 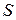обтекается потенциально идеальной жидкостью. Напомним, что потенциальное течение является безвихревым, а производную по нормали можно вычислить как проекцию градиента потенциала на нормаль

.

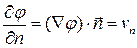Таким образом, граничное условие можно переписать иначе

.

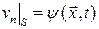Если

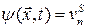
– нормальная скорость поверхности тела 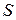, то граничное условие

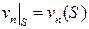
заключается в требовании, чтобы нормальная скорость жидкости на поверхности тела совпадала с нормальной скоростью этой поверхности. Другими словами, жидкость не может проникнуть через поверхность и оторваться от нее. Такое условие называют условием непротекания. Таким образом, задача Неймана описывает безвихревое обтекание тела идеальной несжимаемой жидкостью при условии непротекания жидкости через поверхность тела.