Уравнение теплопроводности для подвижной среды

Пусть

.

Вычислим свертку тензора напряжений с тензором скоростей деформаций

.

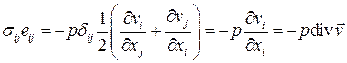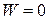Тогда уравнение притока тепла при постоянном и принимает вид

.

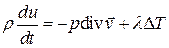Это уравнение можно преобразовать, перейдя к энтальпии

, .

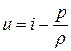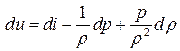Из уравнения неразрывности найдем

.

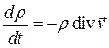В итоге из (2.5.11) получим уравнение теплопроводности для подвижной среды

.

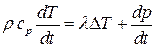Это уравнение уже нужно решать совместно с уравнениями неразрывности и импульса, а также уравнением состояния, в качестве которого можно взять, например, уравнение состояния совершенного газа. В механике под совершенным газом имеют в виду идеальный калорически совершенный газ, для которого выполняются следующие соотношения:

уравнение Клапейрона-Менделеева

,

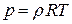соотношения для внутренней энергии и энтальпии

, .

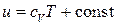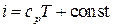3. Некоторые модели и теории
механики сплошной среды

Рассмотрим некоторые модели сплошной среды такие, как идеальная жидкость, ньютоновская жидкость, тело Гука.

Идеальная, вязкая, ньютоновская жидкости

Идеальная жидкость

Сплошная среда называется идеальной жидкостью, если

1) тензор напряжений является шаровым

;

2) плотность является функцией давления и температуры 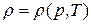, причем повышение давления 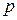вызывает повышение плотности 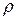, а повышение температуры вызывает понижение плотности .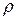

Если в рассматриваемом процессе плотность является функцией одного давления 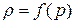, то жидкость называется баротропной. Тогда можно ввести функцию давления

,

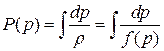для которой

, .

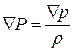Для идеальной жидкости тензор напряжений является шаровым, следовательно, изотропным. Матрица тензора напряжений имеет вид

,

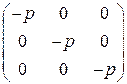где 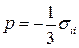. Главные напряжения равны между собой и равны .

Если тензор шаровой, то любой единичный вектор является его главной осью. Поэтому на любой площадке с нормалью 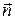вектор напряжений имеет вид

.

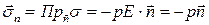Следовательно, , , 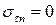т.е. нормальное напряжение равно (с противоположным знаком) давлению, касательных напряжений нет.

Отсутствие касательного напряжения – основное свойство идеальной жидкости. Давление на любой площадке не зависит от ее ориентации. Во многих случаях вода и воздух ведут себя как идеальные жидкости, так как обладают малой вязкостью.

Построим математическую модель течения идеальной жидкости. Для этого в систему уравнений движения

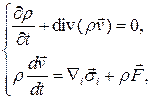
подставим тензор напряжений для идеальной жидкости

.

Для замыкания системы не хватает уравнения для давления 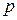. Во многих случаях можно принять условие несжимаемости жидкости, считать, что плотность не зависит от давления. Реальные жидкости обладают большой теплоемкостью, в отличие от газов. Поэтому часто можно пренебречь зависимостью 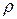от и считать, что 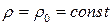. Тогда уравнение неразрывности будет иметь вид

,

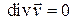то есть относительная скорость изменения материального объема равна нулю. Получили модель идеальной несжимаемой жидкости

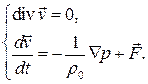
Решим эту систему уравнений в одномерном случае. Пусть , тогда

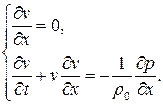
Можно исключить из системы скорость и получить уравнение для давления. Продифференцируем первое уравнение по 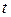, второе – по 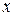. Получим:

.

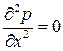Решение уравнения имеет вид

,

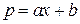где и 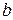в общем случае могут зависеть от времени .

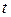Рис. 3.1.1

Если задать давление на входе и выходе (Рис. 3.1.1), то для фиксированного момента времени изменение давления вдоль трубы задается формулой

.

Условие несжимаемости можно применять к дозвуковым течениям, когда скорость потока много меньше скорости звука в среде.

Рассмотрим две задачи для идеальной жидкости.