Закон сохранения энергии. Будем рассматривать сплошную среду как термодинамическую систему, изменение состояния которой обусловлено обменом энергией как между материальными частицами
Будем рассматривать сплошную среду как термодинамическую систему, изменение состояния которой обусловлено обменом энергией как между материальными частицами среды, так и с внешними телами и полями.
Состояние системы может быть равновесным или неравновесным. При равновесии все локальные параметры системы с течением времени не изменяются. Переход из неравновесного состояния в равновесное называется процессом релаксации.
Равновесное состояние характеризуется конечным числом параметров. Для однородных жидкостей и газов такими параметрами являются плотность 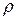 или удельный объем
или удельный объем  , давление
, давление 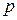 и абсолютная температура
и абсолютная температура 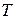 . Они связаны уравнением состояния
. Они связаны уравнением состояния

Поэтому независимыми являются любые два из трех параметров.
Важной характеристикой термодинамической системы является внутренняя энергия, равная суммарной энергии микродвижения молекул. Обозначим через 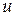 удельную (единицы массы) внутреннюю энергию сплошной среды. Другой характеристикой является кинетическая энергия, равная суммарной энергии макродвижения материальных частиц среды со скоростью
удельную (единицы массы) внутреннюю энергию сплошной среды. Другой характеристикой является кинетическая энергия, равная суммарной энергии макродвижения материальных частиц среды со скоростью 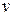 . Кинетическая энергия единицы массы среды равна
. Кинетическая энергия единицы массы среды равна 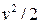 , а единицы объема –
, а единицы объема –  . Полная удельная энергия (единицы массы) сплошной среды равна
. Полная удельная энергия (единицы массы) сплошной среды равна
 .
.
Обмен энергией между рассматриваемым телом и другими телами происходит за счет совершения работы и обмена теплом. Работой  называют количество энергии, переданное телом при силовом воздействии на внешние тела. Если
называют количество энергии, переданное телом при силовом воздействии на внешние тела. Если  , то тело совершает работу и его энергия уменьшается. Если
, то тело совершает работу и его энергия уменьшается. Если 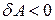 , то работа совершается над телом и его энергия растет. Внешний теплообмен характеризуется количеством теплоты
, то работа совершается над телом и его энергия растет. Внешний теплообмен характеризуется количеством теплоты 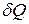 . Если
. Если  , то тело получает тепло, и отдает его, если
, то тело получает тепло, и отдает его, если 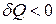 .
.
Первое начало термодинамики гласит, что количество тепла, сообщенное системе, идет на приращение внутренней энергии и совершение системой работы над внешними телами
 .
.
Для равновесной системы с уравнением состояния работа равна
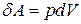 .
.
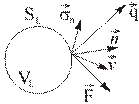 Рис. 2.5.1
Рис. 2.5.1
| Рассмотрим материальный объем 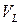 с поверхностью с поверхностью 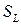 (Рис. 2.5.1). (Рис. 2.5.1).
|
Согласно закону сохранения энергии скорость изменения во времени полной энергии материального объема равна сумме работы в единицу времени (мощности) действующих на объем внешних массовых и поверхностных сил, притока к объему тепла и других видов энергии немеханической природы.
Запишем баланс полной энергии для материального объема 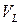 .
.
 .
.
Изменение полной энергии тела 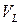 происходит за счет работы внешних поверхностных сил, внешних массовых сил, внешнего теплообмена и взаимодействия с внешними полями, не связанного с движением частиц тела (например, поглощение электромагнитного или оптического излучения, намагничивание, электрическая поляризация и т.д.). Каждый фактор задается соответствующим интегралом справа. Здесь
происходит за счет работы внешних поверхностных сил, внешних массовых сил, внешнего теплообмена и взаимодействия с внешними полями, не связанного с движением частиц тела (например, поглощение электромагнитного или оптического излучения, намагничивание, электрическая поляризация и т.д.). Каждый фактор задается соответствующим интегралом справа. Здесь 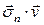 – мощность внешних поверхностных сил на единицу площади,
– мощность внешних поверхностных сил на единицу площади,  – мощность внешних массовых сил в единице объема,
– мощность внешних массовых сил в единице объема,  – поверхностная плотность внешнего потока тепла в единицу времени,
– поверхностная плотность внешнего потока тепла в единицу времени, 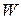 – массовая плотность потока энергии немеханической природы в единицу времени.
– массовая плотность потока энергии немеханической природы в единицу времени.
Получим балансовое уравнение полной энергии в дифференциальной форме. Для этого преобразуем интегральное уравнение аналогично тому, как это делали при получении уравнений неразрывности, импульса, момента импульса. К интегралу слева применим формулу дифференцирования, к поверхностным интегралам применим соответствующие формулы Гаусса-Остроградского, предварительно представив вектор напряжений в виде
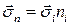 .
.
Тогда
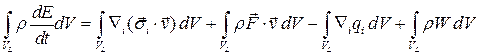 .
.
В силу произвольности объема 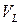 и теоремы 1 получим дифференциальное уравнение полной энергии
и теоремы 1 получим дифференциальное уравнение полной энергии
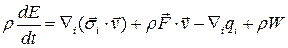 .
.
Заметим, что для приведения этого уравнения к дивергентной форме следует воспользоваться аналогом дивергентной формы ускорения
 .
.
Запишем закон сохранения энергии для контрольного объема 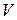 . Для этого воспользуемся формулой , связывающей производные по времени от интегралов по материальному и контрольному объемам, и уравнением . Получим
. Для этого воспользуемся формулой , связывающей производные по времени от интегралов по материальному и контрольному объемам, и уравнением . Получим

Если контрольный объем неподвижен, то 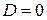 .
.
Так же, как в случае законов сохранения массы, количества движения и момента количества движения, из уравнения можно получить дифференциальное уравнение баланса энергии .
Дата добавления: 2015-12-29; просмотров: 1059;
