Главные оси и главные напряжения
Тензор напряжений 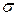 – это симметричный тензор второго ранга. Поэтому, как выше показано, он имеет три вещественных главных значения
– это симметричный тензор второго ранга. Поэтому, как выше показано, он имеет три вещественных главных значения 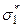 ,
, 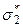 и
и 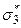 . Им соответствуют три главные оси
. Им соответствуют три главные оси 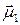 ,
,  и
и  . Если в качестве базиса системы координат взять главные оси
. Если в качестве базиса системы координат взять главные оси 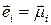 , то тензор напряжений будет иметь диагональный вид
, то тензор напряжений будет иметь диагональный вид
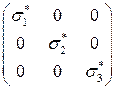 ,
,
то есть на площадках с нормалями, являющимися базисными векторами этой системы координат, есть только нормальные напряжения.
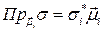 (по
(по 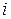 не суммировать!).
не суммировать!).
Нормальные напряжения 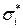 (
( 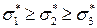 ) называются главными напряжениями. Вектор напряжений на произвольной площадке с нормалью
) называются главными напряжениями. Вектор напряжений на произвольной площадке с нормалью 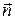 можно выразить через главные напряжения
можно выразить через главные напряжения
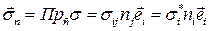 .
.
Состояние сплошной среды называется одноосным напряженным состоянием, если 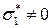 ,
, 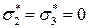 (если
(если 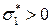 , то происходит одноосное растяжение, если
, то происходит одноосное растяжение, если 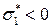 , то сжатие). Соответственно, двухосное напряженное состояние:
, то сжатие). Соответственно, двухосное напряженное состояние: 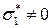 ,
, 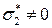 ,
, 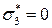 . Трехосное напряженное состояние:
. Трехосное напряженное состояние:  .
.
Важной характеристикой напряженного состояния среды является первый инвариант
 .
.
Давлением 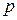 называется величина
называется величина
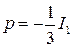 .
.
Тензор напряжений можно представить в виде суммы двух тензоров
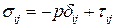 .
.
В этой сумме первое слагаемое есть шаровой тензор, второе слагаемое называется девиатором. Такое представление тензора напряжений удобно для изучения свойств сплошной среды.
Отсюда следует выражение для девиатора тензора напряжений
 .
.
Например, для тензора напряжений, приведенного к главным осям, разложение на шаровой тензор и девиатор имеет вид
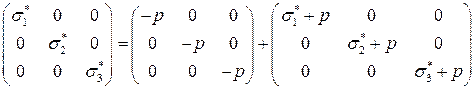
Дата добавления: 2015-12-29; просмотров: 1612;
