Закон сохранения количества движения
Основным динамическим соотношением механики сплошной среды является закон сохранения количества движения, согласно которому скорость изменения количества движения любого материального объема равна главному вектору всех действующих на него внешних массовых и поверхностных сил.
 Рис. 2.3.1
Рис. 2.3.1
| Рассмотрим материальный объем 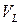 , ограниченный поверхностью , ограниченный поверхностью 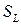 (Рис. 2.3.1). Тогда, согласно закону сохранения количества движения, (Рис. 2.3.1). Тогда, согласно закону сохранения количества движения,
|
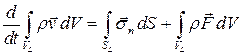
где 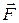 – массовая плотность внешних массовых сил.
– массовая плотность внешних массовых сил.
Если проинтегрировать уравнение по времени, то оно будет иметь вид
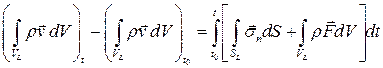 .
.
Правая часть уравнения представляет собой импульс внешних сил за время  , поэтому оно называется уравнением импульсов.
, поэтому оно называется уравнением импульсов.
Получим дифференциальное уравнение количества движения или балансовое уравнение импульсов. Для этого продифференцируем интеграл по подвижному объему 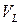 , выразим вектор напряжений
, выразим вектор напряжений 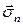 через базисные векторы напряжений
через базисные векторы напряжений 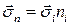 и применим к поверхностному интегралу обобщенную теорему Гаусса-Остроградского. Получим
и применим к поверхностному интегралу обобщенную теорему Гаусса-Остроградского. Получим
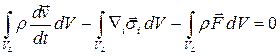 .
.
В силу произвольности объема 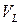 , согласно теореме 1 параграфа 1.7.1, получим векторное дифференциальное уравнение импульсов
, согласно теореме 1 параграфа 1.7.1, получим векторное дифференциальное уравнение импульсов
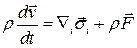 ,
,
или три скалярных в проекциях на 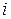 -ю ось
-ю ось
 ,
, 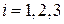 .
.
Уравнение импульсов можно записать и для контрольного объема 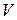 , который в момент времени
, который в момент времени 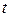 совпадает с материальным объемом
совпадает с материальным объемом 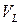 . В силу следствия 3 из теоремы 3 параграфа 1.7.1
. В силу следствия 3 из теоремы 3 параграфа 1.7.1
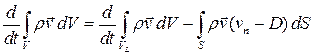 .
.
В силу уравнения получим
 .
.
Если контрольный объем неподвижен, то 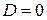 . Из интегрального уравнения можно еще раз получить дифференциальное уравнение импульсов .
. Из интегрального уравнения можно еще раз получить дифференциальное уравнение импульсов .
Так же, как в случае уравнения неразрывности, можно получить уравнение импульсов для одномерного случая в лагранжевых переменных
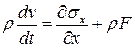 ,
,
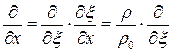 ,
,
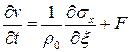 .
.
Могут быть полезны и другие формы записи уравнения импульсов, которые можно получить с помощью следующих равенств.
1. Дивергентная форма записи ускорения
 .
.
2. Формула Громеки-Ламба для ускорения
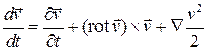 .
.
Проанализируем полученную для описания движения сплошной среды систему уравнений неразрывности и импульсов
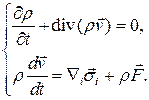
В этой системе четыре скалярных уравнения и 13 неизвестных – 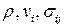 . Для замыкания необходимы 9 уравнений. Для этого можно использовать уравнения состояния или реологические законы, определяющие тензор напряжений
. Для замыкания необходимы 9 уравнений. Для этого можно использовать уравнения состояния или реологические законы, определяющие тензор напряжений 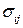 и учитывающие характерные механические свойства среды. В общем случае может понадобиться привлечь термодинамику, электродинамику и физико-химическую кинетику.
и учитывающие характерные механические свойства среды. В общем случае может понадобиться привлечь термодинамику, электродинамику и физико-химическую кинетику.
Дата добавления: 2015-12-29; просмотров: 1957;
