Уравнение неразрывности при лагранжевом описании
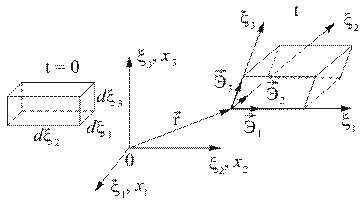 Рис. 1.7.3
Рис. 1.7.3
|
Рассмотрим материальную частицу в форме прямоугольного параллелепипеда (Рис. 1.7.3) с ребрами
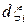 ,
, 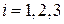 .
.
Объем материальной частицы в момент 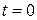
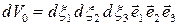 .
.
В момент времени 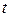 эта частица деформируется и станет косоугольным параллелепипедом с ребрами
эта частица деформируется и станет косоугольным параллелепипедом с ребрами 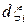
 , его объем будет равен
, его объем будет равен
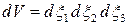
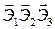 ,
, 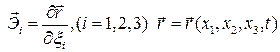 .
.
Так как деформации малы, то отрезок переходит в отрезок, но возможно другой длины, углы между ребрами параллелепипеда изменяются. Но длина ребер параллелепипеда в материальных координатах не изменяется!
Вычислим смешанное произведение векторов 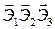
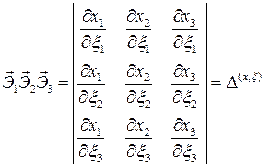 .
.
Перепишем выражение для объема:
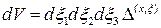 .
.
Вычислим отношение объемов
 .
.
Масса параллелепипеда не изменилась
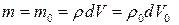 .
.
Отсюда получим
 ,
,
 ,
, 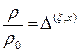 .
.
Отсюда ясен механический смысл якобиана 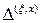 : якобиан, вычисленный в некоторый момент времени, равен отношению плотности частицы в текущий момент времени к плотности частицы в начальный момент времени.
: якобиан, вычисленный в некоторый момент времени, равен отношению плотности частицы в текущий момент времени к плотности частицы в начальный момент времени.
Уравнение неразрывности при лагранжевом описании в дифференциальной форме следует из и имеет вид
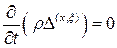
Для одномерного случая
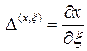 ,
,
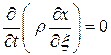 ,
,
 .
.
Таким образом, уравнение неразрывности в лагранжевых переменных для одномерного движения имеет вид
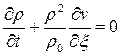 .
.
Данное уравнение можно получить и непосредственно из уравнения неразрывности в эйлеровых переменных
 ,
,
которое в одномерном случае выглядит так
 .
.
Заменим  на
на  , тогда производная
, тогда производная 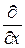 заменится на производную
заменится на производную  :
:
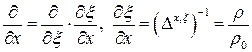 .
.
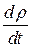 – это материальная производная, при лагранжевом описании она вычисляется как частная производная. Получим
– это материальная производная, при лагранжевом описании она вычисляется как частная производная. Получим
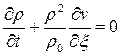 .
.
Дата добавления: 2015-12-29; просмотров: 1505;
