Замечание. Обобщение формулы Гаусса-Остроградского
В математическом анализе формула Гаусса-Остроградского доказана в следующем виде
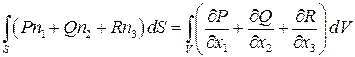 .
.
Покажем, что формула будет верна, если скалярные функции 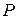 ,
, 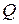 и
и 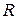 заменить на векторные
заменить на векторные 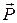 ,
, 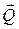 и
и 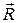 .
.
Для доказательства каждую векторную функцию 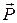 ,
, 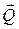 и
и 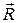 надо разложить по базису и применить указанную формулу к каждой компоненте
надо разложить по базису и применить указанную формулу к каждой компоненте
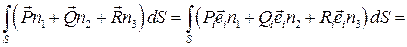
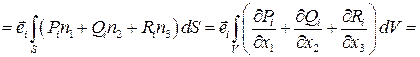
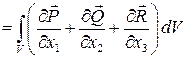 .
.
Итак, формула справедлива как для скалярных, так и для векторных функций 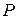 ,
, 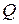 и
и 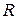 .
.
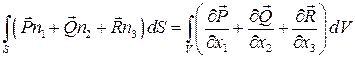 .
.
В дальнейшем нам понадобятся понятия контрольного объема (поверхности), скорости поверхности, переноса параметра сплошной среды через поверхность и правило дифференцирования по времени интеграла по подвижному пространственному объему.
Контрольным объемомназывается выделенный объем пространства 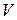 , его граница
, его граница 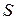 называется контрольной поверхностью.
называется контрольной поверхностью.
Для определения скорости поверхности 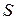 в некоторой точке
в некоторой точке 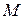 рассмотрим положения поверхности
рассмотрим положения поверхности 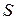 в два момента времени:
в два момента времени: 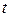 и
и 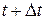 (Рис. 1.7.1). Выберем окрестность точки
(Рис. 1.7.1). Выберем окрестность точки 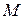 , площадку
, площадку 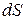 и проведем в точке
и проведем в точке 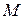 внешнюю нормаль
внешнюю нормаль 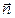 . Отрезок нормали между поверхностями
. Отрезок нормали между поверхностями 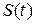 и
и 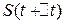 обозначим
обозначим 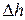 . Скоростью перемещения поверхности
. Скоростью перемещения поверхности 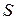 в точке
в точке 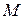 называется
называется
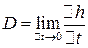 .
.
Переносом параметра 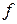 через площадку
через площадку 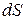 с нормалью
с нормалью 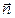 называют величину, равную
называют величину, равную
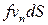 ,
,
где 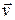 – скорость сплошной среды,
– скорость сплошной среды, 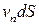 – секундный расход среды через
– секундный расход среды через 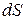 . Перенос через поверхность
. Перенос через поверхность 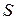 определяется интегралом
определяется интегралом
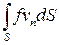 .
.
Теорема 3. (О дифференцировании интеграла по подвижному объему).
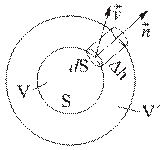 Рис. 1.7.1
Рис. 1.7.1
| Рассмотрим пространственный объем 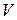 , ограниченный поверхностью , ограниченный поверхностью 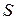 (Рис.1.7.1). Имеет место формула (Рис.1.7.1). Имеет место формула
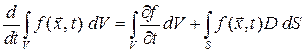
|
где 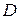 – скорость поверхности
– скорость поверхности 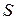 ,
, 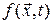 – произвольная функция.
– произвольная функция.
◄ Рассматриваемый объем в момент времени 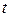 обозначим
обозначим 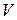 , а в момент времени
, а в момент времени 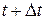 –
– 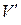 .
.
Представим объем 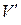 в виде
в виде
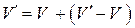 .
.
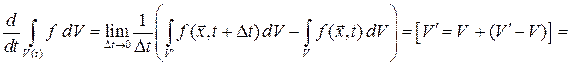
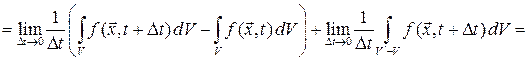
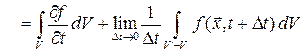 .
.
Разобьем объем 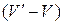 на цилиндры с основанием
на цилиндры с основанием 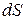 и высотой
и высотой 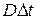 (Рис. 1.7.1). Объем цилиндра с основанием
(Рис. 1.7.1). Объем цилиндра с основанием 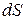 и высотой
и высотой 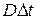 равен
равен
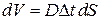 .
.
Тогда интеграл по объему 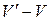 можно преобразовать в интеграл по поверхности
можно преобразовать в интеграл по поверхности 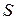 :
:
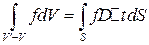 ,
,
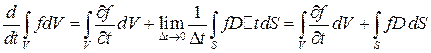 . ►
. ►
Следствия.
1. Пусть объем 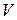 является материальным,
является материальным, 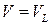 ,
, 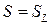 , тогда скорость поверхности
, тогда скорость поверхности 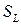 равна
равна 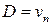 , где
, где 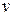 – скорость сплошной среды, и формула дифференцирования принимает вид
– скорость сплошной среды, и формула дифференцирования принимает вид
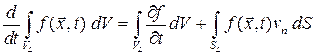 .
.
2. Используя теорему Гаусса-Остроградского, формулу можно переписать иначе:
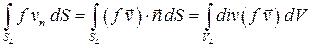 .
.
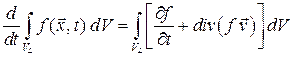 .
.
3. Если предположить, что в момент времени 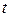 контрольный объем
контрольный объем 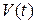 совпадает с материальным
совпадает с материальным
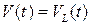 ,
, 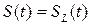 ,
,
то из формул и следует
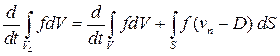
Замечание. Получим еще одну формулу дифференцирования интеграла по материальному объему, когда подынтегральная функция имеет вид
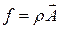 ,
,
где 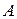 – скалярная или векторная функция.
– скалярная или векторная функция.
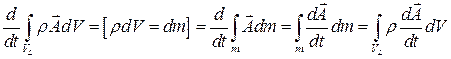 .
.
Обратим внимание, что под интегралом стоит материальная производная, так как при интегрировании параметр 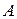 вычисляется для фиксированной материальной частицы
вычисляется для фиксированной материальной частицы 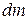 .
.
Итак,
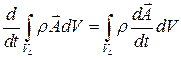 .
.
Дата добавления: 2015-12-29; просмотров: 1661;
