Механический смысл тензора малых деформаций
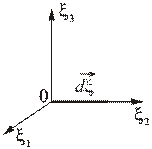 Рис.1.5.4
Рис.1.5.4
| Пусть материальный элемент в момент времени 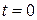 расположен вдоль оси расположен вдоль оси 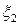 , как показано на Рис.1.5.4. В этом случае , как показано на Рис.1.5.4. В этом случае 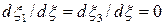 , , 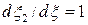 . .
|
Поэтому относительное его удлинение
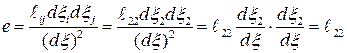 .
.
Итак, 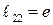 , то есть относительное удлинение материального элемента, первоначально расположенного вдоль направления
, то есть относительное удлинение материального элемента, первоначально расположенного вдоль направления 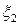 равно компоненте
равно компоненте 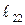 . Точно так же для элементов, первоначально лежащих вдоль осей
. Точно так же для элементов, первоначально лежащих вдоль осей 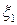 и
и 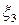 , их относительные удлинения равны
, их относительные удлинения равны 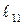 и
и 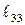 соответственно.
соответственно.
Таким образом, диагональная компонента тензора малых деформаций численно равна относительному удлинению вдоль соответствующей оси координат.
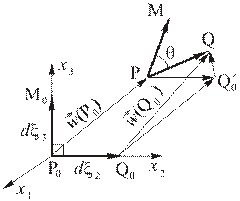 Рис. 1.5.5
Рис. 1.5.5
| Рассмотрим деформацию сдвига, т.е. изменение угла между материальными элементами, которые первоначально лежат вдоль двух осей координат. Пусть после деформации отрезок 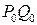 перешел в отрезок перешел в отрезок 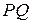 , ,
|
а отрезок 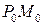 перешел в отрезок
перешел в отрезок 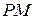 (Рис. 1.5.5). Угол между этими векторами, первоначально прямой, перешел в угол
(Рис. 1.5.5). Угол между этими векторами, первоначально прямой, перешел в угол 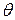 . Обозначим изменение этого угла как
. Обозначим изменение этого угла как
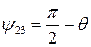 .
.
Тогда 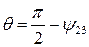 .
.
Разложим перемещение (функцию) 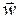 в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 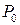 :
:
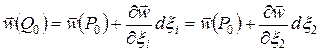 ,
,
так как 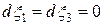 для точки
для точки 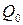 .
.
Построим векторы 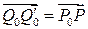 ,
, 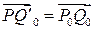 .
.
Выразим 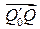 через перемещение
через перемещение
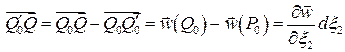
тогда
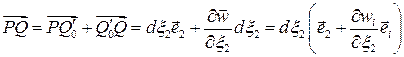 .
.
Аналогично,
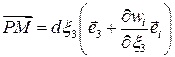 .
.
Вычислим скалярное произведение векторов 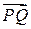 и
и 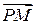 :
:
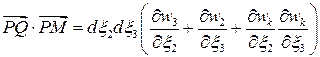 .
.
В линейном приближении, в силу малости деформаций:
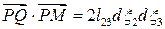 .
.
С другой стороны,
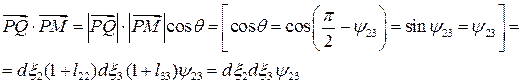
в линейном приближении, в силу малости деформаций.
Таким образом,
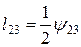 .
.
Аналогично можно показать, что 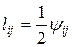 ,
, 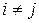 .
.
Таким образом, недиагональная компонента тензора малых деформаций численно равна половине изменения первоначально прямого угла между соответствующими осями координат
Замечание. В силу симметричности тензор деформаций имеет три вещественных главных значения, называемые главными деформациями. В любой точке тензор малых деформаций можно привести к главным осям, и он будет иметь диагональный вид, то есть в любой точке существуют три взаимно перпендикулярных волокна, которые при деформации изменяют лишь свою длину, но остаются взаимно перпендикулярными.
Вычислим относительное изменение объема материальной частицы. Для простоты рассмотрим частицу в форме шара. Расположим центр шара в начале координат. В качестве осей координат возьмем главные оси тензора малых деформаций. Вследствие выбора осей координат, при деформации не произойдет скашивания углов, т.е. шар перейдет в эллипсоид.
Вычислим относительное изменение объема 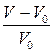 .
.
Пусть радиус шара равен 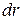 , тогда
, тогда 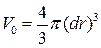 .
.
Вычислим объем шара после деформации в линейном приближении относительно 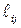 :
:
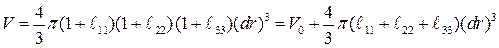 .
.
Тогда
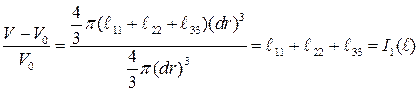 ,
,
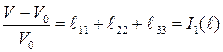 .
.
Вычислим первый инвариант тензора малых деформаций 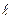 через перемещения:
через перемещения:
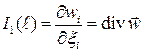 .
.
Если 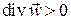 , то объем шара увеличивается, и наоборот.
, то объем шара увеличивается, и наоборот.
Таким образом, первый инвариант тензора малых деформаций – дивергенция вектора перемещения – численно равен относительному изменению малого материального объема сплошной среды.
Дата добавления: 2015-12-29; просмотров: 2181;
