Условия совместности деформаций

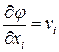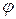Сначала поясним смысл понятия условия совместности на примере потенциального течения. Если поле скоростей потенциальное, то , где – потенциал. Если смотреть на систему 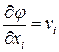как на систему относительно неизвестных скоростей, то имеем три уравнения относительно трех неизвестных. Следовательно, система всегда имеет решение.

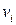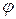Если же заданы , но неизвестно, то система переопределена и может не иметь решения.

Скорость потенциального течения должна удовлетворять условию 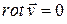. Это условие можно назвать условием совместности скоростей потенциального течения. Оно обеспечивает разрешимость задачи по нахождению потенциала.

Таким образом, условия совместности – это некоторые дополнительные условия разрешимости задачи.

Для малых деформаций 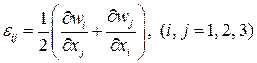. Тензор малых деформаций в силу симметрии имеет шесть различных компонент. Если перемещения заданы, то из этой системы всегда можно найти деформации: .

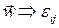Наоборот, если заданы деформации и необходимо найти перемещения ( 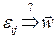), то система становится переопределенной (6 уравнений относительно трех неизвестных). Условия, при которых эта задача решается, называются условиями совместности деформаций (деформации должны быть такими, чтобы не нарушалась сплошность среды, т.е. чтобы материал не «порвался» и чтобы не образовалось «складок»). Условия совместности являются условиями реализуемости заданных деформаций сплошной среды.