Эйлеров и лагранжев тензоры деформаций
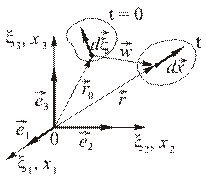 Рис.1.5.1
Рис.1.5.1
| Деформация– это изменение взаимного расположения материальных частиц сплошной среды, которое вызывает изменение сил взаимодействия между материальными частицами. |
Деформация малой окрестности некоторой точки определяется изменением длины и поворотом любого материального волокна (отрезка), исходящего из этой точки (Рис.1.5.1), то есть простейшими деформациями является относительное удлинение и сдвиг.
Для описания деформационного движения сплошной среды нужно определить изменение длины и поворот любого материального волокна. Пусть 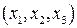 – пространственная декартова система координат с базисом
– пространственная декартова система координат с базисом 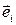 и
и 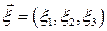 – материальные координаты частицы, равные ее пространственным координатам в начальный момент времени, то есть
– материальные координаты частицы, равные ее пространственным координатам в начальный момент времени, то есть 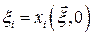 ,
, 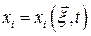 – закон движения частицы.
– закон движения частицы.

|
Рис. 1.5.2
Материальным элементом с началом в частице 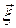 и соответствующим вектору
и соответствующим вектору 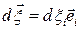 называется совокупность частиц, заполняющих бесконечно малый отрезок и имеющих лагранжевы координаты в пределах от
называется совокупность частиц, заполняющих бесконечно малый отрезок и имеющих лагранжевы координаты в пределах от 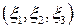 до
до 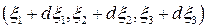 (Рис. 1.5.2).
(Рис. 1.5.2).
В текущий момент времени 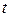 положение материального элемента определяется положением
положение материального элемента определяется положением 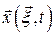 его начальной точки
его начальной точки 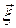 и вектором
и вектором
 .
.
Для определения изменения длины составим выражение для квадратов длины материального элемента  в начальный
в начальный 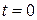 и
и 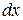 в текущий
в текущий 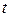 моменты времени:
моменты времени:
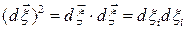 ,
,
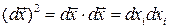 .
.
Найдем изменение квадрата длины в лагранжевых переменных. Так как 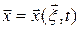 , то
, то
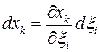 ,
,
 .
.
Составим выражение для изменения квадрата длины материального элемента:

Выражение 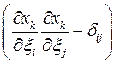 не зависит от конкретного материального элемента (волокна).
не зависит от конкретного материального элемента (волокна).
Тензор 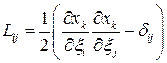 называется лагранжевым тензором деформаций (тензором деформаций Грина).
называется лагранжевым тензором деформаций (тензором деформаций Грина).
Таким образом, изменение квадрата длины материального элемента выражается через лагранжев тензор деформаций:
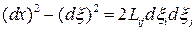 .
.
Теперь выразим изменение квадрата длины материального элемента в эйлеровых переменных. В этом случае 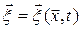 ,
,
 ,
,
 ,
, 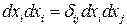 ,
,
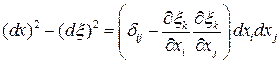 .
.
Тензор 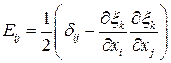 называется эйлеровым тензором деформаций (тензором деформаций Альманси).
называется эйлеровым тензором деформаций (тензором деформаций Альманси).
Изменение квадрата длины материального элемента выражается через эйлеров тензор деформаций:
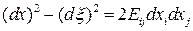 .
.
Итак,
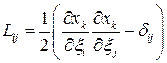 ,
, 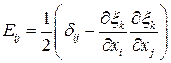 ,
,
 .
.
Легко видеть, что тензоры деформаций являются симметричными тензорами 2-го ранга.
Получим формулы для вычисления тензоров L и E через перемещение материальной частицы 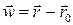 (Рис.1.5.3).
(Рис.1.5.3).
 Рис.1.5.3
Рис.1.5.3
|
1. Лагранжево описание:  ,
, 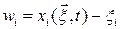 .
.
Для вычисления лагранжева тензора конечных деформаций необходимы производные 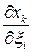 . Выразим эти производные через производные перемещения:
. Выразим эти производные через производные перемещения:
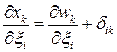 .
.
Подставим их в выражение для тензора:
 .
.
Окончательно получаем:
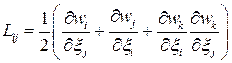
2. Эйлерово описание: 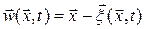 ,
,  .
.
Аналогично, если выразить производные 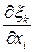 через производные перемещения, эйлеров тензор конечных деформаций примет вид:
через производные перемещения, эйлеров тензор конечных деформаций примет вид:
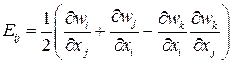 .
.
Дата добавления: 2015-12-29; просмотров: 3481;
