Операции над тензорами
Сложение: T =P +S 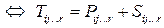 .
.
Умножение тензора на число: T = λP 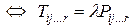 .
.
Диадным произведением двух векторов 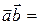 T называется тензор второго ранга с компонентами
T называется тензор второго ранга с компонентами 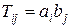 .
.
Диадным произведением базисных векторов 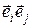 является тензор второго ранга T, матрица которого имеет один ненулевой элемент
является тензор второго ранга T, матрица которого имеет один ненулевой элемент 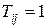 .
.
Полиадным произведением тензора второго ранга T на вектор 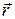 называется тензор третьего ранга с компонентами
называется тензор третьего ранга с компонентами
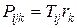 .
.
В общем случае, при полиадном произведении ранг произведения равен сумме рангов сомножителей.
Заметим, что диадное и полиадное произведения являются некоммутативными операциями.
Тензор второго ранга, так же, как и вектор, можно разложить по базису, причем базис состоит из девяти тензоров 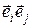 :
:
T 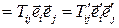 .
.
Умножение со сверткой.Умножение со сверткой тензоров 1-го ранга представляет собой скалярное произведение, результатом которого является тензор нулевого ранга
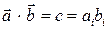 .
.
Умножение со сверткой тензоров 2-го ранга дает в результате скаляр и определяется как
T·S 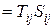 .
.
Умножение со сверткой тензора 2-го ранга на вектор дает в результате вектор и определяется как
T· 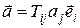 .
.
Заметим, что последняя операция является некоммутативной, т.к.
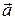 ·T
·T 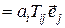 .
.
Проекцией тензора T на единичный вектор 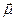 называется вектор, который вычисляется как
называется вектор, который вычисляется как
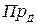 T
T 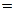 T·
T· 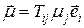 .
.
Заметим, что компонентами проекций тензора на базисные векторы являются соответствующие столбцы матрицы тензора. Например,T 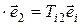 – вектор, компоненты которого расположены во 2-м столбце матрицы
– вектор, компоненты которого расположены во 2-м столбце матрицы 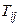
Введем определения некоторых тензоров второго ранга специального вида.
Симметричный тензор: 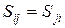 .
.
Антисимметричный тензор: 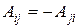 .
.
Теорема 1. Любой тензор можно представить в виде суммы симметричного и антисимметричного тензоров. Это представление единственно.
◄ Доказательство следует из равенства
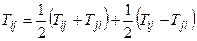 .
.
Единственность доказывается методом от противного. ►
Теорема 2. Симметричный (антисимметричный) тензор при любом ортогональном преобразовании остается симметричным (антисимметричным).
◄ Доказательство. 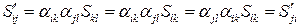 . Аналогично,
. Аналогично, 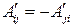 . ►
. ►
Транспонированный тензор:
TT 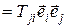 .
.
Свойства:
1. если тензор S симметричный, то ST=S
2. 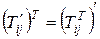
Тензор Кронекера: 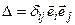 .
.
Шаровым называется тензор S=λ∆.
Изотропным называется тензор T, если
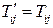 .
.
Дата добавления: 2015-12-29; просмотров: 3581;
