Потенциальное и вихревое движения
Поле скорости называется потенциальным, если существует такая функция 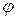 , что
, что 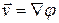 . Функция
. Функция 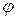 называется потенциалом скорости.
называется потенциалом скорости.
Движение сплошной среды называется потенциальным, если поле скорости является потенциальным.
Поле скорости называется безвихревым, если 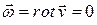 . В противном случае, когда
. В противном случае, когда 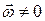 , движение называется вихревым. По аналогии с линией тока для вихревого движения вводится понятие вихревой линии. Вихревой линией называется векторная линия вектора вихря
, движение называется вихревым. По аналогии с линией тока для вихревого движения вводится понятие вихревой линии. Вихревой линией называется векторная линия вектора вихря 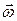 . Уравнение вихревой линии имеет вид:
. Уравнение вихревой линии имеет вид:
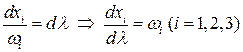 .
.
Вихревой поверхностью (трубкой) называется поверхность, состоящая из вихревых линий, проведенных через каждую точку некоторого контура, не являющегося вихревой линией.
Для вихревого движения имеет место формула Стокса: поток вихря поля скорости через поверхность S, ограниченную замкнутым контуром L, равен циркуляции поля вокруг контура L
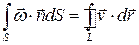 .
.
Из теоремы следует, что для потенциального течения ( 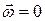 )
)
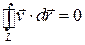 .
.
Условие потенциальности течения доказывается в следующей теореме.
Теорема. Поле скорости является потенциальным тогда и только тогда, когда оно безвихревое.
◄ Необходимость. Дано, что
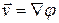 ,
,
отсюда следует, что
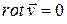 .
.
Достаточность. Дано, что
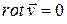 .
.
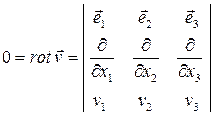 ,
,
то есть координаты вектора вихря равны нулю:
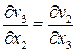 ,
, 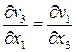 ,
, 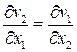 .
.
Согласно теореме математического анализа, если функции 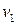 ,
, 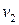 и
и 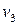 удовлетворяют выписанным выше равенствам, то существует функция
удовлетворяют выписанным выше равенствам, то существует функция 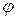 такая, что
такая, что
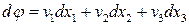 .
.
По определению
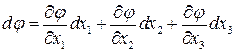 ,
,
следовательно,
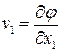 ,
, 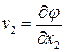 и
и 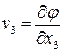 .
.
Отсюда следует, что
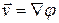 . ►
. ►
Примеры потенциальных движений.
1. Поступательное движение
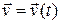 .
.
Легко убедиться, что потенциалом скорости будет функция
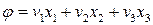 .
.
2. Одномерное движение
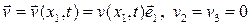
Легко убедиться, что
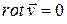 .
.
Построим потенциал 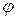 . По условию
. По условию 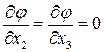 , следовательно,
, следовательно, 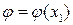 ,
, 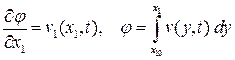 .
.
3. Источник (сток)
Чтобы построить потенциал скорости жидкости, сначала нужно получить выражение для скорости. Пусть скорость жидкости зависит от расстояния до центра и от времени 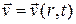 . Тогда в сферической системе координат эта задача является одномерной.
. Тогда в сферической системе координат эта задача является одномерной.
Пусть 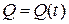 – расход жидкости через некоторую сферическую поверхность радиуса
– расход жидкости через некоторую сферическую поверхность радиуса 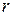 . Ее площадь
. Ее площадь
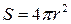 ,
, 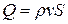 .
.
где 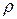 – плотность жидкости.
– плотность жидкости.
Жидкость будем считать несжимаемой Для простоты положим 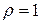 . Тогда
. Тогда
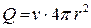 .
.
Отсюда
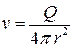 ,
, 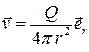 ,
, 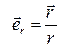 .
.
Легко убедиться, интегрируя скорость по радиусу, что потенциал скорости
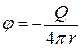 .
.
Дата добавления: 2015-12-29; просмотров: 2590;
